Hesaplayan adam: Yılbaşını havada kovalamak

Uzun bir aradan sonra tekrar merhabalar. Geçen macerada hesaplayan adam olarak dünyanın dönüşüyle yerçekimi arasındaki rekabeti incelemiştik. Bu macerada da dünyanın kendi etrafında dönüşüyle devam ediyoruz.

Zorunlu seyahat planlarımdan ötürü 2015 yılbaşı gecesini havada geçirdiğim süreç boyunca, ne pilotun ne de mürettebatın yılbaşı konusunda hiç bir anons yapmaması beni hayalkırıklığına uğratmıştı. Havada hareket halinde olduğumuz için içinde bulunduğumuz yerel saat sürekli değişiyordu, ama uçuş sırasında hangi anda yerel saatin 00:00 olduğunu kabaca hesaplamak o kadar da zor değildi. Ben de iş başa düştü deyip kağıt kalemi elime aldım.

Önce problemi daha detaylı tanımlayayım: Yerel saatle 18:30’da ABD’nin Washington kentinden kalkan bir uçak Almanya’nın Frankfurt am Main kentine doğru yol alıyor. Uçak ABD’den kalktığında Avrupa’nın batı kıyısındaki yerel saat zaten geceyarısına yakın olduğu için yılbaşı okyanus üstünde bir yerlerde beni yakalamalı. Peki 8 saatlik bu uçuşun hangi anında ve de yeryüzünde nerede yerel saat 00:00 olmalı? Dünya dönerken, hayali geceyarısı çizgisi de (saatin 00:00 olduğu çizgi) doğudan batıya, yani Avrupa’dan ABD’ye doğru ilerliyor. Diğer taraftan, içinde bulunduğum uçak ise batıdan doğuya doğru yol alıyor. Dolayısıyla ben ve gece çizgisi, yolda karşı yönlerden birbirine doğru yaklaşan iki taşıt gibiyiz.

Varsayımlar

Öncelikle 3 varsayım yapmak zorundayım. Dileyen bu varsayımların yerine daha gerçekçi modeller kurup, hesapları kendine göre zorlaştırabilir.

• Hız: Uçağın pistte hızlanmaya başladığı andan, havadaki azami hızına ulaştığı ana kadar geçen süre (15 dakika civarı) boyunca sahip olduğu hızı sabit ve seyir hızı olarak farzedeceğim. Aksi takdirde, uçağın en baştan itibaren an be an hızını bilip toplam katettiği mesafeyi integral alarak hesaplamak zorundayım. Elimde bu veri olmadığı için, uçağın hızını sabit alacağım.
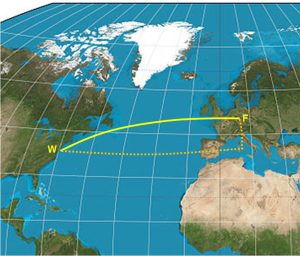
• Rota: Dünya’nın küresel bir şekle sahip olması aslında Öklid dışı geometri (elliptik geometri) kullanmamı gerektiriyor [1]. Hayali dikey çizgiler olan boylamlar her zaman birbirlerine paralel olsalar da kutuplara doğru daralıp bir nokta halinde birleşirler. Dolayısıyla, 50. enlem üzerinde 8 saat uçtuktan sonra ulaşılan nokta 30. enlem üzerinde uçtuktan sonra ulaşılan noktadan daha ileride olur. Hem elliptik geometri konusunda yetkin olmadığım için, hem de hesapları basit tutmak adına, katedilen mesafenin boylamlara dik yani enlemlere parallel olduğunu farzedeceğim (resim 1’deki yatay kesikli çizgi gibi). Eğer uçuş Washington DC – Frankfurt gibi birbirine nispeten bu kadar yakın enlemlerde olan iki şehir yerine Brezilya-İsveç gibi kuzey güney yönünde çok uzak olan iki şehir arasında uçsaydı, bu varsayım pek mantıklı olmayacaktı.
• Dünyanın eğikliği ve Güneş’e olan konumu: Dünyanın eksen eğikliği 23 derece civarında olduğu ve güneş etrafında asimetrik bir yörünge izledği için, gece yarısı çizgisi aslında özel günler haricinde boylamlara paralel olmuyor. Ben ise gece yarısı çizgisini bir boylam gibi enlemlere dik farz edeceğim. Bu ihmal sırasında olabilecek hata payı belirli günlerde 30 dakikaya kadar çıkabilirken, 31 Aralık gecesi 4 dakika civarında kalacağı için çok dert etmiyorum [2].

Gerekli bilgiler

Yukarıdaki varsayımlardan başka bir de şu bilgilere ihtiyacım olacak:

• Uçağın hızı sabit ve saatte 650 kilometre.
• Dünyanın çapı 6380 kilometre.
• Washington’un enlem ve boylamı: 39° kuzey, 77° batı
• Frankfurt’un enlem ve boylamı: 50° kuzey, 9° batı
• Washington ve Frankfurt arası kuş uçuşu mesafe 6526 km
• Yerel kalkış saati 18:30

Bundan sonrası ise bolca dört işlem.

Hesap vakti

Öncelikle iki enlem ve iki boylam arasındaki mesafeleri hesaplayacağım. Tanım olarak, enlemler arasındaki mesafe yeryüzündeki her yerde sabit olduğu için, dünyanın çevresinin yarısını direkt 180’e bölerek (toplam 90 kuzey ve 90 güney enlemi var) 111 km buluyorum. Bu mesafe 77. batı boylamında da, 9. doğu boylamında aynı.

İşin zor kısmı ise boylamlar arasındaki mesafeleri hesaplamakta, çünkü bu mesafeler 39. ve 50. kuzey enlemlerinde farklı. En uzun mesafe Ekvator’da iken (Ekvator’un uzunluğunun 360’a bölümü olan 111 km), Ekvator’dan kuzeye ve güneye gidildikçe boylamlar arasındaki mesafe daralıyor. Washington 39° kuzey enlemine sahip. Bunun kosinüs değerini dünyanın çevresiyle çarpıp 39. kuzey enlemi çemberinin çevresi olan 4950 km’yi buluyorum. Bu çember tabii ki ekvator çemberinden (6370 km) daha dar. Bu çemberi de 360 boylam eşit olarak keseceği için boylamlar arasındaki mesafe de 86,4 km olacak. Aynı hesabı Frankfurt’un yer aldığı 50. kuzey enlemi için yaparsam bu mesafe 71,5 km çıkıyor. Bu mesafeler niye bu kadar önemli diye soracak olursanız, sebebi uçuş sırasında katedilen mesafeye göre kaçıncı boylamda olduğumuzu bulmak zorunda olmamız.

Hesabın son aşaması ise gece yarısı çizgisini yakalamak. Burada deneme-yanılma yoluyla çözüme gideceğim. Diyelim ki uçuşa başlayalı 2 saat olmuş. Bu süre boyunca uçak 1900 km yol katetmiş olacak. Eğer iki boylam arasındaki mesafe 86,4 km olsa ve uçağın hep 39. kuzey enleminde uçtuğu farzedilirse bu 22 boylam geçildiği anlamına geliyor. Aynı hesabı 71,5 km bazında hesaplarsam 27 boylam yapıyor. Gerçekte ise uçağın rotası enlemler arasında geçiş yapacağı için 22 ile 27 arasında bir değer olmalı bu, çünkü katedilen mesafenin bir kısmı enlemler arasında harcanacak. Ben de hesabı daha fazla karmaşıklaştırmayıp ortalama olarak 24 boylam geçildiğini farzediyorum. Her biri 4 dakikadan 24 boylam yerel saatin kalkış noktasına nispeten 96 dakika ileride olması demek. Bunun üstüne katedilen 2 saatlik uçuş süresini de eklersem (yazının başında belirttiğim gibi ben ve geceyarısı çizgisi karşı yönlerden yaklaşıyoruz) 216 dakika yapar, yani yerel saat 22:06.

Eğer kalkıştan 3 saat 10 dakika sonrasını aynı şekilde hesaplarsam, 34 boylam geçilmesi sonucu yerel saatin 23:55 olduğu 43° batı boylamını buluyoruz, yani Atlas Okyanusu’nun ortalarında bir yer. Güney yarıkürede yer alan Brezilya’nın doğu kıyıları da bu boylama oldukça yakın. Sonuç olarak Rio ile aynı anda yılbaşına girdiğimi söyleyebilirim.

Bu hesaplama sırasında yaptığım çeşitli varsayımların işimi kolaylaştırdığı açık. Yine de en büyük kolaylığın uçtuğum rotadan kaynaklandığını unutmamamız lazım. Rotamı enlemlere paralel farzettim uçuş süresini katedilen mesafeye direk oranlayabilmemi sağladı. Eğer doğu-batı yönünde uçulan mesafeye kıyasla kuzey-güney yönünde çok daha uzun bir mesafe katetmiş olsaydım, küresel yüzeyler için uygulanan trigonometrik hesaplara dalmam gerekecekti [4].

Kaynaklar

Kapak resmi: http://upload.wikimedia.org/wikipedia/commons/thumb/9/91/Winkel_triple_projection_SW.jpg/1024px-Winkel_triple_projection_SW.jpg

1. http://en.wikipedia.org/wiki/Elliptic_geometry
2. http://en.wikipedia.org/wiki/Equation_of_time
3. http://upload.wikimedia.org/wikipedia/commons/thumb/9/91/Winkel_triple_projection_SW.jpg/1024px-Winkel_triple_projection_SW.jpg
4. http://www.movable-type.co.uk/scripts/latlong.html