Merhabalar. “Hesaplayan Adam” olarak size her ay basit gibi gözüken ama biraz kafa yorduran ufak hesaplar yapacağım. Serinin ilk yazısında yerçekimi kuvvetini ve bunun etkisinden kurtulmanın yollarını farazi olarak hesaplayacağım.
Beni bu yazıyı yazmaya iten iki olayın ilki lastik ördek şeklindeki 67P/Churyumov–Gerasimenko adlı kuyruklu yıldıza zor bela inen Rosetta uzay aracıydı. Diğeri ise geçenlerde izlediğim Interstellar filmindeki Endurance adlı kendi etrafında dönerek yapay yerçekimi oluşturan uzay istasyonuydu. Yazının sonunda bu konulara da değineceğim.
Yerçekimi kuvveti
Bu senaryoda bizi ilgilendiren iki kuvvet var: Yerçekimi kuvveti ve merkezkaç kuvveti. Yerçekimi kuvveti Newton’un formüle ettiği gibi:

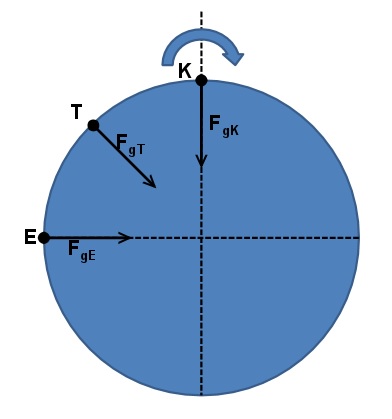
Burada Fg hesaplamak istediğim yerçekimi kuvveti, My yeryüzünün kütlesi olan 5,972E24 kg (E 10 üzeri demek, yani neredeyese 6 trilyon kere trilyon kilogram), Mh benim kütlem (bunun önemsiz olduğunu göstereceğim), G ise evrensel çekim sabiti (6,67E-11 Nm2/kg2 yani 66,7nin trilyonda biri) ve bu değer evrenin her yerinde aynı. Son olarak r de yeryüzünün merkeziyle benim aramdaki mesafe. Eğer ayaklarım yere basıyorsa, yeryüzünün ortalama yarıçapı olan 6378 km olacak r’nin değeri. Eğer yeryüzünden oldukça uzaklaşıyorsam, tabii bu mesafeyi 6378 km ile toplamak zorundayım. Gördüğünüz gibi, değerleri ve birimleri yerine koyunca yerçekimi kuvveti N, yani Newton cinsinden elime geçiyor. Yeryüzünde 1 kiloluk bir kütlenin ağırlığı 9,8 N’dir. Bu yüzden dünyadaki yerçekimi ivmesi, yani g kuvveti, 9,8 m/s2’dir. Bu bilgiyi yazının sonunda kullanacağım. Burada önemli olan bir nokta yerçekimi kuvvetinin her zaman iki kütlenin merkezlerini birleştiren doğrultuda olduğu (Şekil 1). O yüzden dünyadaki herkesin ayakları yere eşit miktarda basar. Yani yerçekimi herkese adildir.
Merkezkaç kuvveti
İşin ikinci perdesi merkezkaç kuvveti. Bir ipe bağlı bir cismi çevirince ipi geren, ya da arabayla virajı dönerken bizi koltuğa yaslayan kuvvetten bahsediyorum. Onun da formülü şu şekilde:

Burada Fc merkezkaç kuvveti (birimi yine Newton). Mh benim kütlem, v ise dönüş sırasındaki doğrusal hızım (aşağıda detaylı açıklayacağım), rc ise benimle dönüş ekseni arasındaki mesafe, ki bu dünyanın neresinde olduğuma göre değişir.
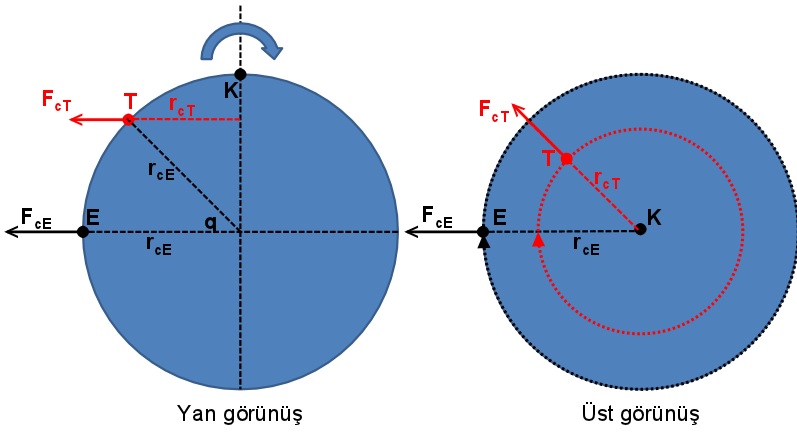
Doğrusal ve açısal hız kavramları ile devam edelim. Dünyaya kuzey-güney kutup doğrultusunda bakacak olursak (Şekil 2, üst görünüş), yeryüzündeki bütün noktalar birim zaman içinde aynı açıyı süpürür. Yani 24 saatte 360 derece. Buna istisna sadece iki nokta var, onlar da güney ve kuzey kutup noktalarının kendileri çünkü bu noktalarda açısal hız sıfır (bu noktalarda gece ve gündüz olmasının sebebi ise dünyanın eksen eğikliğidir).
Yeryüzündeki her noktada açısal hızın aynı olmasıyla beraber farklı enlemlerdeki noktaların doğrusal hızları farklı olmak zorunda, çünkü bu noktaların dönüş eksenine uzaklıkları farklı. E noktası tam ekvatorda olduğu için eksenden en uzak mesafeye ve dolayısıyla en yüksek doğrusal hıza sahip. T noktası ise dönüş eksenine daha yakın, dolayısıyla doğrusal hızı daha düşük. Doğrusal hızın enleme göre değişimini enlem değerinin kosinüsünü kullanarak hesaplayabilirim.
Ayağımız yerden kesilsin
Bu hesabın temelini oluşturan iki kuvveti de tanımladıktan sonra bunları nasıl kullanacağıma geldi sıra. Burada dikkat edilmesi gereken nokta merkezkaç ve yerçekimi kuvvetlerinin birbirlerine eşit olmaları ki, beni yeryüzüne bağlayan bir kuvvet kalmasın.
Eğer kutup noktalarında olsaydım, üstümdeki yerçekimi kuvvetini etkisiz kılacak bir merkezkaç kuvveti olmayacaktı, çünkü dönüş ekseninin tam üstünde yer alacaktım, bir başka değişle açısal ve çizgisel hızlarım sıfır olacaktı (Şekil 2). Eğer ekvator hizasında olsaydım, merkezkaç kuvveti ve yerçekimi kuvveti birbirleriyle aynı doğrultuda ama ters yönde olacaklardı. Bunun dışında, yeryüzündeki herhangi bir noktada ise bu kuvvetler birbirleriyle aynı yönde olmayacakları için merkezkaç kuvvetinin etki ettiği enlem derecesine göre kosinüs değerini almak zorundayım (Şekil 3).

Şu anki haliyle yeryüzündeki merkezkaç kuvveti en şiddetli olduğu nokta olan ekvatorda bile yerçekimi kuvvetinin sadece binde üçüne denk geliyor. Dolayısıyla yerçekiminden kurtulmam için ya yeryüzünden uzaklaşmam, ya dünyayı daha hızlı döndürmem, ya da dünyanın kütlesini azaltmam gerekiyor. Şimdi bu üç durumu ele alalım.
1) Dünyaya olan mesafe
Ekvator hizasından başlayarak dünyadan H kadar uzaklaştığımızı varsayalım, böylece işlemleri trigonometri kullanmadan yapabilirim. Yerçekimi ve merkezkaç kuvvetlerini birbirlerine eşitlersem şu durum ortaya çıkıyor:

Burada r dünyanın yarıçapı, H de uzaklaşma miktarım. v, yani çizgisel hızımız ise dünyanın açısal hızı (24 saatte 360 derece yani 2 pi radyan) çarpı eksene olan toplam uzaklık yani r+H. Dolasıyla burada tek bilinmeyen olan H değeri için denklemi çözersek yuvarlak olarak 36 bin kilometre değerini buluyoruz. Küsüratına kadar aynı olmasa da jeostatik yörünge değerine oldukça yaklaşık bir değer buluyoruz, ki bu tesadüf değil. Bu mesafede yer alan uydular, dünya çevresinde dünya ile aynı açısal hızda döndüklerinde, gökyüzünde sabit bir nokta olarak kalırlar ve yeryüzüne düşmeden hareketlerine devam ederler. Eğer ekvator dışında bir noktadan başlayarak yeryüzünden uzaklaşsaydım, iki durum ortaya çıkacaktı:
- Eğer yeryüzü ile yine aynı eksen etrafında dönseydim mesafemi 36 bin kilometreden daha da fazla arttırmam gerekecekti. Mesela temeli yeryüzünde olan bir uzay asansörü hayal edelim. Eğer bu asansör Türkiye’den uzaya gitseydi, 36 bin değil de ancak 48 bin kilometrede yerçekiminin etkisi ortadan kalkacaktı. Bunun sebebi, Türkiye’de dünyanın dönüş eksenine ekvatordan daha yakın olmam.
- Diğer taraftan, Türkiye’den kalkan bir uzay aracı ile dünyadan uzaklaşıp dünyanın dönüş ekseni etrafında değil de Türkiye ve Türkiye’nin anitpod noktasına (yeryüzüne Türkiye’den bir şiş soktuğunuzu farzedin, şişin diğer taraftan çıktığı nokta Türkiye’nin antipodudur) dik bir eksen etrafında dünya ile aynı açısal hızda dönseydim, 36 bin kilometre mesafe yine yeterli olacaktı (Şekil 4).

2) Dünyanın açısal hızı
Bu sefer dünyadan uzaklaşmadığımı, yani yeryüzünde kaldığımı düşünelim. Bu durumda dünya şu andakindan daha hızlı dönmeli ki, merkezkaç kuvveti yüzlerce kat daha yüksek olsun, ve yerçekimi beni tutamasın.

Burada ry yeryüzünün yarıçapı, rc dünyanın dönüş eksenin olan mesafe (bulunduğum yerin enlemine bağlı), w ise tek bilinmeyenimiz olan dünyanın açısal hızı. Eğer bu denklemi ekvatordaki bir nokta için çözersek, dünyanın kendi çevresinde neredeyse 17 kat hızlı dönmesi gerekecekti. Yani bir gün 85 dakika sürecekti. Bu hızda Türkiye’de ise yerçekimi etkisini yarı yarıya kaybedecekti. Bir başka deyişle neredeyse yarı ağırlıkta olacaktım. Eğer Türkiye’de yerçekiminden kurtulmak isteseydim dünyanın 25 kat hızlı dönmesi gerekecekti. Bu hızda ekvatorda ise yeryüzünden kopmamak için yerin 21 kilometre altında olmam gerecekti.
3) Dünyanın kütlesi
Son olarak yine yeryüzünde kaldığımı ve dünyanın kendi etrafında 24 saatte döndüğünü kabul edip, dünyanın kütlesi ile oynayacağım. 4 numaralı denkleme dönersek, Bu koşulda tek bilinmeyenimiz olan My için denklemi çözmemiz gerekecekti (rc yine enleme bağlı). Eğer yeryüzünün boyutu bu haliyle kalsaydı, ama ortalama yoğunluğu 290 kat daha az olsaydı (yani suyun yoğunluğunun ellide biri kadar), ekvatordaki yerçekimi kuvveti şu anki merkezkaç kuvvetiyle aynı büyüklükte olacaktı. Türkiye’de bu durumun oluşması için ise yeryüzünün ortalama 620 kat daha az bir yoğunluğa sahip olması gerekecekti. Bu durumda ekvatorda yeryüzünden kopmamak için yerin 4 kilometre altında olmam gerekecekti.
Yeryüzünün yoğunluğunu azaltmak yerine, bu haliyle bırakıp (metreküp başına ortalama 5510 kg), boyutunu artırmayı veya azaltmayı denersem yerçekimi kuvvetinin her halükarda merkezkaç kuvvetine üstün geldiğini buluyorum.
Ekstra
Bu kadar hesap yaptıktan sonra yazının başında belirttiğim iki olayı irdelemek istiyorum. Lastik ördek şeklindeki kuyrukluyıldıza çarpıp seken Rosetta uzay aracının durumu aslında açık. İnmeye çalıştığı cisim o kadar küçük ki (1E13 kg yani dünyanın 600 milyarda biri kadar), yerçekimi kuvveti yok denecek kadar küçük. Eğer bir astronot yüzeye inebilseydi, adım atmaya çalışırken bile kuyrukluyıldızdan kopacaktı. Buna karşılık, hatırlarsanız Armageddon filmindeki göktaşına ayak basan astronotların bir güreş tutmadıkları kalmıştı.
Son olarak Interstellar filminde yer alan Endurance uzay istasyonundaki yapay yerçekimi ortamının mümkün olup olmadığına bakalım. Senaryoya göre 64 metre çapındaki bu istasyon dakikada 5,6 tur dönüyor. Bu durumda (4) numaralı denklemin sağ tarafını kullanırsak, istasyonda yapay olarak oluşturulan yerçekimi ivmesi değerini 11 buluyoruz, ki yeryüzünde 9,8 olan bu değere oldukça yakın. Eğer 32 yerine 28,5 metrelik bir mesafe alırsak, 9,8 değerine zaten ulaşıyoruz, ki oldukça makul. Kısacası senaristler astrofiziğe kafa yorarken, böyle basit ama önemli bir detayı da gözardı etmemişler.
Sonraki macera: Yılbaşını havada kovalamak
Kaynaklar
Kapak resmi: http://en.wikipedia.org/wiki/File:Earth_in_vivid_colors_1.jpg
Şekiller yazar tarafından Açık Bilim için hazırlanmıştır.


kutuplarda çizgisel hız sıfır mı oluyor? o zaman orada yerçekimi nasıl etki ediyor??
Yazida da belirttigim gibi “Eğer kutup noktalarında olsaydım, üstümdeki yerçekimi kuvvetini etkisiz kılacak bir merkezkaç kuvveti olmayacaktı, çünkü dönüş ekseninin tam üstünde yer alacaktım, bir başka değişle açısal ve çizgisel hızlarım sıfır olacaktı (Şekil 2).” Dolayisiyla yercekimi hicbir sey olmamis gibi beni tutmaya devam edecekti.
Bir kabloyu gökyüzüne doğru yukarıda tutabilseydik (uzay asansörü) bu kablo dengede durabilmesi için ucuna ne kadarlık bir ağırlık takılması gerekir?
Bu kablo 100 km uzunluğunda olsa ve ucunda 100 ton ağırlık olsa etki eden merkezkaç kuvveti ne olurdu mesela?
Jeostatik denge için uzunluk ve ağırlık dengesi nasıl olmalı?
Jeostatik denge için 36.000 km uzağa çıkmaya gerek olmadığını düşünüyorum.
Jeostatik denge derken jeostatik yörüngeden bahsediyorsak, bu yörünge bir tanedir ve yeryüzünden 36000 km civarı uzaklıktadır. Makalede bunun hesaplamasını yapmıştım. Çözülen denklemin matematiksel olarak tek bir cevabı var, o da 36000 kmdir.
100 kmlik homojen bir kablonun ağırlık merkezi yeryüzünden 50 km uzaklıktadır. Kabloya bağlı 100 tonluk cisim de yeryüzünden 100 km uzaklıktadır. Dolayısıyla bu iki kütlenin (kablo ve cisim) ortalama ağırlık merkezi 50. ve 100. km arası bir noktadadır (kütleleri biliyorsak bu noktanın yerini hesaplayabiliriz).
Uzay asansörü tasarımında (https://tr.wikipedia.org/wiki/Uzay_asans%C3%B6r%C3%BC) kablo ucuna bağlanacak cismin jeostatik yörüngeden daha uzak bir mesafede olması gerekiyor, öyle ki kablo+cismin ortalama ağırlık merkezi yeryüzünden tam 36000 km uzaklıkta olsun. Çünkü tam bu mesafede kablo+cisim üzerindeki yerçekimi ve merkezkaç kuvvetleri birbirini dengeler, böylece uzay asansörü yeryüzüne düşmeden uzayda asılı kalır. Bağlanacak cismin ağırlığı da bu durumda kullanılacak kablonun toplam ağırlığına bağlı oluyor.
matematik doğrudur fakat bu fizik değil. merkezkaç kuvveti yoktur. hareket sonucu sanal kuvvetler ortaya çıkmaz. merkeze dik merkezcil kuvvet ve dünyanın dönüş hızı buna dik olacak şekilde (teğet) tekrar bileşke kuvvet hesaplamalısınız.
Merhabalar. Merkezkac ve merkezcil kuvvetlerin tanimi konusunda “fizik kanunlari cercevesinde” hak veriyorum. Aradaki fark burada biraz daha iyi anlatilmis.
https://tr.wikipedia.org/wiki/Merkezka%C3%A7_kuvveti
https://tr.wikipedia.org/wiki/Merkezcil_kuvvet
Ama dediginiz gibi yeni vektorler cizersek, yine ayni sonuca ulasmamiz lazim. Burada NASA’nin benzer bir hesap yaptigini görÿoruz.
https://www-spof.gsfc.nasa.gov/stargaze/Srotfram1.htm
Ayni sekilde, dönüs eksenine dik bir “merkezkac kuvveti” (ing. centrifugal force) hesaplaniyor.
cevabınız için çok teşekkürler.
Formül 1 e göre yerçekimi dünya üzerinde her yerde aynı demişsiniz. Fakat ekvator ve kutuplara göre yarıçap yani kütlelesin merkezleri arasındaki fark 21.385m. Dolayısıyla hesap biraz karışıyor orada. Çok büyük farklar değil elbette ama bunu ararken yazınıza denk geldiğim için gözüme çarptı. Yazı için emeğinize sağlık
Haklisiniz. Yalniz, bu hesaplar sirasinda o kadar cok varsayim ve yuvarlama yapiyoruz ki, yaricaplar arasindaki 21 metrelik farkin pek bir önemi kalmiyor. Yorum icin tesekkür ediyorum.
ÇOK FAYDALANDIM TEŞEKKÜR EDERİM ALLAH CC İLMİNİZİ VE BİLMİNİZİ ARTTIRSIN. CENNETE EVVELA İLİM VE BİLİM ADAMLARI ALİMLER GİRECEK 4 KİTAP EMRİ BUDUR . SAYGILARIMLA. AV. İSMAİL BEŞİKTEPE BURSA
Tesekkurler yorumunuz icin.
tam kutup noktasında k noktasında durdugumuzda kendi etrafımızda mı dönüyoruz? o zaman çevredeki yıldızları sürekli etrafımızda dönüyor olarak görmemiz gerekmez mi?
Evet, dediginiz gibi kendi etrafimizda donuyoruz. Tabi bu donus 24 saat surdugu icin bize oldukca yavas geliyor ve sonuclarini farketmiyoruz.
Kutup noktasinda ya da yerkure ustunde baska bir noktada farketmez, dunya kendi etrafinda dondugu icin, yildizlar da bizim etrafimizda donuyor gibi gozukur. Internette “time lapse photography of stars” diye gorsel aratirsaniz, bu durumu kanitlayan resimler gorursunuz. Dedigim gibi, bu donus oldukca yavas surdugu icin, bize yildizlarin gokyuzundeki yeri sabitmis gibi gelir, halbuki goreceli olarak konumlarimiz degisir, ve gokyuzunde bize gore bir cember cizerler.
Yer çekimi diye birşey yok. Uzay itimi var.
Bağımsız her hangi iki cisim arasında bir çekim kuvveti olduğunda, o iki cisim muhakkak bu çekim kuvvetlerinin etki ettiği yönde bir birine doğru, çekim kuvvetleride Artarak çekilirdi.
Örneğin uzay boşluğunda iki pinpon topu arasında bir çekim kuvveti olsaydı o toplar birbirlerine doğru, çekim kuvvetleri artarak yaklaşırlar ve birleşirlerdi. Dünya ile Ay aralarında bir çekim kuvvetinin gelgit olaylarındaki etkisini cekim kuvveti olarak açıklayabilirmisiniz ?
İki devasa cisim arasında bir çekim kuvveti olsaydı, dünya ve ay herhangi bir noktaya bagli olayan cisimler oldukları için, birbirlerine doğru çekilir ve yaklaştıkça çekim kuvvetleri daha da artar, böylece daha hızlı çekilir, çekim kuvvetleri daha da çok artar, bu böyle, iki cisim çarpışana kadar devam ederdi.
Ayin çekim kuvveti sebebi ile Denizler kabarmiyor. Ay dünyanın hangi tarafındaysa, o yönde evrenin itim kuvveti dalgalarını bir miktar kırıyor.
Dünyanın dönüş hızı ile de denizler kabariyor. Aksi olsaydı sular aya doğru 1 metre cekilmisse, dünyanin çekim alanından uzaklaşmış ve aya daha çok yakalamış oldukları için, ayin çekim kuvvetinden daha çok etkilenerek daha çok yükselir, bu da böyle bütün denizler uzaya doğru çekilene kadar devam ederdi.
Masa üzerinde iki pinpon topu düşünün.
İki top masa üzerinde bağımsız duruyorlar. Evren itim kuvveti uyguluyor. Toplara nefesimizi ufluyoruz, iki topta aynı yönde ve kendi çenelerinde de dönerek hareket etmeye başlıyorlar. aralarındaki mesafede hemen hemen aynı. Evrenin itme kuvveti,
similasyonda toplara uyguladığımız nefesle ayni şey olarak düşünün, iki topun birbirlerine bakan yüzlerindeki itme kuvveti daha az olur, ve denizler bu şekilde kabarır.
Yani ayin dunyaya bakan yüzü ile ona en yakin yeryüzü noktası arasında evrenin itme kuvveti daha azdır.
50cm³ hacminde iki akvaryum düşünün, bu iki akvaryumu suyla doldurup tam ortalarına birer pinpon topu yerleştirdigimizi varsayalım. sonra bu iki akvaryumu birleştirip 1m³ lük bir akvaryum oluşturalım. yukarıdan, aşağıdan, doğu, batı, kuzey ve güneyden , her iki topta kendilerine göre eşit mesafede. Bu akvaryumu hareket ettirmeye başladığınızda toplar bir birine yaklaşmaz. Çünki evrenle birlikte hareket ediyorlardir. Bu iki cismin arasindan geçecek şekilde akvaryuma bir cisim bırakırsak iki pinpon topuda birbirinden az da olsa uzaklaşır. ama aralarinda bir çekim olsaydı iki cisimde akvaryumun içinde bir birine doğru çekilir ve birleşirdi. Evrendeki itim kuvveti de toplara her yönden eşit miktarda baskı uygulayan akvaryumdaki su gibidir. bu itme kuvvetidir. tüm yönlerden pinpon toplarını saran akvaryumdaki su gibidir. Bu yüzden itme kuvveti her yönden eşit olduğu için , cisimler yörüngelerinde dönerken birbirilerine doğru çekilip çarpışmazlar.. yani bizim yenmemiz gereken etki yerçekimi değil, kullanmamız gereken güç uzay itimidir.
Hahaha. Ay’ı ya da daha yapılabilir olan uydu araçlarının seyir hızını düşür de gör bakalım uzay itiyor mu?
Yorumunuz icin tesekkürler.
Düsüncelerinizi biraz daginik anlatmissiniz, mümkün oldugunca toparlamaya ve kisa bir cevap vermeye calisacagim.
1) Öncelikle uzay itimi diye bir kavramdan benim haberim yoktu. Bu konuda objektif bir yabanci kaynak biliyorsaniz, adresini bizimle paylasir misiniz? Eger gravitational wave olgusuna deginiyorsaniz, klasik fizikten uzaklasiyoruz ve Einstein’in görelilik teorilerine giriyoruz, ki bu da konumuz degil. Biz elimizdeki sorunu burada klasik mekanik modelleri kullanarak aciklamaya calisiyoruz.
2) “X var, Y yok” diyebilmek X ve/veya Y kavramlarinin varlik/yokluklarini hem hicbir fizik kanununu cignemeden, hem de tekrarlanip onaylanacabilecek deneyler yaparak göstermek gerekir. Aksi taktirde böyle keskin ifadeler kullanmak bir seyin varligini veya yoklugunu kanitlamaya yetmez.
3) Newton’un evrensel kütlecekim yasasi bir klasik fizik yasadir ve bunun makroskopik evrendeki varligini inkar etmek pek mantiga sigmaz (bkz. https://tr.wikipedia.org/wiki/Newton%27un_evrensel_k%C3%BCtle_%C3%A7ekim_yasas%C4%B1). Kuantum seviyesinde bu kütlecekim kanununun calismadigini biliyoruz (bkz. madde 1), ama konumuz su anda kuantum degil, makroskopik evren.
4) Kainatta kütlesi olan her cisim birbirini ceker. Ama Newton’un kütlecekim formülüne de dikkat ederseniz, kücük objeler icin bu cekim kuvveti o kadar kücüktür ki, pratikte yok denecek kadar azdir. Bu kütlecekim kuvveti anca gezegen boyutlarina ciktigimizda gözle görülür bir etki gösterir. Dolayisiyla, bahsettiginiz pinpon toplari birbirini cekiyor, ama onlarin yuvarlanmasini engelleyen yüzey sürtünme kuvvetleri var, suyun icinde onlarin ilerlemesini engelleyen su moleküllerinin brownian hareketleri var, hatta pinpon toplarinin yüzeyindeki elektrostatik yük de onlarin birbirine yaklasmasini engeller. Bu tür etmenleri göz ardi etmissiniz.
5) Dünya ve ay da birbirini ceker, hatta günesle de birbirlerini cekerler. Ama ay dünya etrafindaki, dünya da günes etrafindaki elliptik dönme hareketlerinden dolayi olusan ve kendilerini merkezden disari dogru iten merkezcil kuvvetler sayesinde birbirlerine yapismadan (denge halinde) hareketlerine devam ederler. Gelgit olaylari ve ayin etkisi ise vikipedide gayet güzel aciklanmis, tekrar burada anlatmanin bir katkisi yok (https://tr.wikipedia.org/wiki/Gelgit).
6) Son iki paragraftaki deneylerinizi (masadaki pinpon toplari ve akvaryumlar) anlayamadim, kusura bakmayin. Biraz kili kirk yarmak olacak ama, akvaryumlarin seklinden (kup mu, kuresel mi) bahsetmemissiniz. Ayrica, sekli ne olursa olsun, iki ayri akvaryumun merkezinde yer alan iki pinpon topu tek bir akvaryuma kondugunda her taraftan birbirlerine ayni mesafede olamazlar. Sanirim parcacik simulasyonlarinda sikca kullanilan ve gercekte karsiligi olmayan “periodic boundary conditions” kavramini karistiriyorsunuz (https://en.wikipedia.org/wiki/Periodic_boundary_conditions). Bir de, 50 cm3 hacminde iki akvaryum birlesince 100 cm3 hacme ulasirlar, yani 0.0001 m3, 1 m3 degil.
Çok güzel bir yazı idi, emeklerinize sağlık. Aradığım cevapları buldum. Tam anladığımdan emin olmadığım için bir soru sormak istiyorum. İki cisim gökyüzünden düşüyor olsun, hangi noktada kütleleri önemsiz olarak, eşit hızda düşerler? Böyle bir olasılık var mı? Yerçekiminin merkezkaç kuvvetine yakın olduğu bir yükseklik için atmosferden çıkmak mı gerekir?
Yazıyı beğendiğiniz için teşekkür ederim. Sorularınıza gelince:
1) İki cisim gökyüzünden dünyaya aynı yükseklikten, aynı anda bırakılırlarsa (yani aşağı doğru fırlatılmadan) her zaman eşit hızlarda düşecektir. Bunun sebebi, meşhur yerçekimi ivmesi g’nin tanım olarak dünyanın ve cismin ağırlık merkezlerine etki etmesidir. Dolayısıyla, ne kütlenin ne de yüksekliğin burada bir önemi vardır. Galileo da Pisa kulesinin tepesinden farklı ağırlıkta iki cismi aynı anda bıraktığında, cisimler yere aynı anda çarpmıştı (https://en.wikipedia.org/wiki/Galileo%27s_Leaning_Tower_of_Pisa_experiment).
2) Yerçekiminin merkezkaç kuvvetine eşit ya da yakın olduğu, yazıda hesapladığımız yükseklik olan 36 bin km tanım olarak zaten atmosfer dışıdır. Değişen tanımlardan birine göre dış uzay zaten 100 km sonra başlar (bkz. Karman hattı).
Benim anlamadığım ekvatorda merkezkaç kuvveti yerçekiminin binde üçüne denk geliyorsa hızı neden sadece 17 kat artırıyoruz? 1000 \ 3 kat artırmamız gerekmez mi?
Çünkü merkezkaç kuvveti hızın karesi ile doğru orantılıdır. 1000/3 ün karekökü de 17,3 yapıyor.
Murat Bey; makale için teşekkürler..
Peki bu çekim yasası, şans oyunlarındaki toplarda nasıl çalışır. Bu konuya kafanızı hiç yordunuz mu? Çünkü ben sonraki hafta çıkacak olan rakamların, matematik sayesinde, yüzde doksan oranında, tahmin edilebileceğini düşünüyorum.
Sizin düşünceniz nedir?
Erkan Bey, sınırlı matematik ve fizik bilgimle ilk cevabım bu rakamları önceden bilebilmenin imkansız olduğudur derdim.
Fiziksel olarak topların birbirinden yapısal ve kütlesel hiçbir farkı yok, dolayısıyla bazı toplar mesela daha ağır oldukları için daha diplerde gezinmezdi. Karıştırma süresini de yeterli olarak düşünürsek topların kafese atılış zamanının da bir önemi olmadığını söyleyebiliriz. Matematiksel olarak ise x top arasından y topun seçilme şansı belli.
Burada kafamı karıştıran şey %90 oranıyla neyi kastediyorsunuz? On kere tahmin edip 9unda tutturmayı mı, yoksa seçilecek 10 topun 9unu tahmin etmeyi mi? Bu iki durumda da yine matematiksel hesaplar bellidir ama sonuçta seçilecek sayıları/topları direkman bilebilmek mümkün değildir diyorum.
Konuya dönersek, burada yazdığım denklerle onlarca kütlenin birbiriyle etkileşim halinde olduğu fiziksel bir sistemi çözmek zaten süperbilgisayarlarla yapılan bir hesaplamadır ve kesin çözümü yoktur.
Kütüphanede ders çalışırken kafamda makaledeki gibi bazı sorular belirdi harika bir makale olmuş :) Konu hakkında oldukça bilgili olduğunuz anlattığınız harika anlatımdan görülüyor.Eski bir makale olmasına nazaran yenilerinin artması dileğiyle :)
Beğendiğiniz için teşekkürler. Sonuçlar aslında lise seviyesi temel fizik formülleri ile hesaplanmıştır, ileri düzey bir metot kullanılmamıştır.
Kütle Çekim Kuvveti, Ekvatordan Kutuplara doğru değişmesi gerekir sabit olmaz, çünkü yerçekimi ivmesi değişiyor
Bahadır bey haklısınız, yukarıdaki yorumlardan birinde birinde bu konuyu zaten irdelemiştik. Ama bahsettiğimiz fark oldukça küçük bir miktar dolayısıyla yaptığımız basit hesaplarda kaale almaya değmiyor.
Hesaplamaya şu an üşendim ama kafamda şöyle bir düşünce oluştu. Yazının 3. bölümünün sonunda yapılan şey dünya yrine Jüpiter ve Satürngibigezegenlere uygulandığında ne olur? Yani Jüpiteriele alırsak. Devasa bir yüzey ortalama periyodu ise 9 saat, yoğunluk çok daha düşük. Budurumda Jüpiterin üst atmosferi dediğimiz yeri aslında Jüpiterin kütlesi ve kütleçekimi değil, İçeriğindeki gazların Merkezkaç kuvvetinin gezegenin merkezinden uygun uzaklıkta ve yineort yoğunluğa da bağlı olarak Jüpiterinhızlı dönmesinden kaynaklanan merkezkaç kuvvetinin eşitlenmesi belirlemiş oluyor. Yani Jüpiter daha yavaş dönseydi daha büyük bir kütleye ulaşabilirdi? Daha büyük kütle yani gaz daha fazla sıkışacak ve ort. yoğunluğun da artmasına neden olacaktı. Bu da gaz devleri içersinde neden Jüpiterin Neptünden sonra en yoğun ortalamaya sahip olduğunu ve en yoğun gaz devi Neptün de neden en güneş sistemindeki en hızlı rüzgarların oluşabildiğini gösteriyor olmalı. Ya da kimbilir, yoğunluğu çok düşük ve buna kıyasla neredeyse Jüpiter kadar hızlı dönen Satürn ün çevresinde neden geniş alana yayılan devasa halkaların oluştuğunu??
Yazımdaki hesaplamalarda kütlelerin/gezegenlerin hep katı olarak ele alındığını sanırım belirtmem lazım. Akışkan bir kütleden bahsettiğimiz anda, hele ki kendi etrafında dönen dev bir akışkan kütleden bahsediyoruz, farklı statik ve dinamik etkenler devreye giriyor, mesela akışkanların basınç altında sıkıştırılabilmesi ya da viskoziteden dolayı açısal dönüş hızının merkezden uzaklığa bağlı olarak değişebilmesi gibi.
Gördüğüm kadarıyla Jüpiterin atmosferinde bolca bulunan hidrojen, yerçekimi kuvvetinin büyüklüğünden dolayı olmalı, alt katmanlarda artık sıvıya dönüşüyor. Dediğiniz gibi, Jüpiter daha yavaş dönseydi, herhalde üst katmanlardaki gazlar gezegenin merkezine daha yakın konumlarda olurdu, hatta bunun bir kısmı da sıvıya dönüşüp, gezegenin yüzeyi olarak da sayılabilirdi. Yalnız bu hesap oldukça karmaşık. Hidrojenin basınç altındaki yoğunluk dağılımını bilmek gerekiyor mesela.
Bu arada, ifadenizde bence bir hata var: Şartlar ne olursa olsun (atmosfer uzaya gaz kaçırmadığı yani kütle kaybetmediği sürece) gezegenin toplam kütlesi hep aynı kalacaktır çünkü atmosfer de gezegenin bir parçasıdır. Dönüş hızına göre değişecek değerler sadece gezegenin toplam hacmi ve ortalama yoğunluğu olacaktır.