İki zar attığınızda toplamları iki ile oniki arasında herhangi bir sayı gelebilir. Tavla oynayanlar iyi bilir, zarların toplamı en sık 7 gelir. Bir başka deyişle iki zar attığınızda toplamlarının yedi gelme olasılığı diğer olasılıklardan daha yüksektir. Bu olayları toplamlarına göre sıralayalım. Mesela, toplamın üç olması için hangi zarda 1 hangisinde 2 geldiğinin önemi yok, ama 1-2 ve 2-1 farklı olaylar. Bu durumu sezgisel olarak daha kolay hale getirmek için zarların birini birinci diğerini ikinci zar olarak düşüneceğiz (veya birini kırmızı diğerini mavi gibi birbirlerinden farklılaştıralım).

2 = 1+1
3 = 1+2, 2+1
4 = 1+3, 2+2, 3+1
5 = 1+4, 2+3, 3+2, 4+1
6 = 1+5, 2+4, 3+3, 4+2, 5+1
7 = 1+6, 2+5, 3+4, 4+3, 5+2, 6+1
8 = 2+6, 3+5, 4+4, 5+3, 6+2
9 = 3+6, 4+5, 5+4, 6+3
10 = 4+6, 5+5, 6+4
11 = 5+6, 6+5
12 = 6+6
Olası toplamların dağılımını listeledik, şimdi olasıklarını da hesaplayalım.Toplamda 36 tane olay. Dolayısıyla olasılıkları aşağıdaki gibi hesaplayabliriz:
1/36 olasılıkla toplam 2
2/36 olasılıkla toplam 3
3/36 olasılıkla toplam 4
4/36 olasılıkla toplam 5
5/36 olasılıkla toplam 6
6/36 olasılıkla toplam 7
5/36 olasılıkla toplam 8
4/36 olasılıkla toplam 9
3/36 olasılıkla toplam 10
2/36 olasılıkla toplam 11
1/36 olasılıkla toplam 12
Bu hesaplarda yüzleri (karşılıklı yüzlerin toplamı 7 olacak) şekilde birden altıya kadar numaranlandırılmış standard zarlar kullandığımızı varsaydık.
1977 yılında Amerika’da Buffalo’dan albay George Sicherman yukarıda hesapladığımız dağılımları bir kitapta gördükten sonra merak etti: Yüzleri başka bir şekilde numaralandırılmış ve atıldığında aynı toplamları aynı dağılımla (yani aynı olasılıklarla) veren bir başka zar çifti var mıdır? Kendi sorusunu da cevapladı. Cevap olumluydu. Bulduğu zarları bir mektupla Martin Gardner’a iletti, Gardner da bu soruyu ve Sicherman’ın çözümünü 1977’de Scientific American dergisindeki köşesinden düyaya duyurdu.

Yazının başında toplamların dağılımını hesağladığımız tabloya geri dönelim. Bu tabloda, mesela 2+1 birinci zarın 2, ikincisinin 1 geldiği durumu ifade ediyor. Bu toplamlar üzerinde biraz oyanarak bu toplamları aynı dağılımla veren farklı şekilde numaralandırılmış bir zar çifti bulacağız. Elimizdeki zarların üzerindeki bütün sayıları sildiğimizi varsayalım. Bu zarları yeniden numaralandıracağız.
Toplamın 2 gelmesinin tek bir olasılığı var 1+1, bunu değiştirmemiz mümkün değil. Yani başladığımız zarlarda 1’leri değiştiremeyiz.
Toplamın 3 olması için 1+2 veya 2+1 gelmesi lazım. Birinci toplam 1+2 yerine yeniden 2+1 gelse dağılım değişmez. Yani yeni zar çiftinde 1+2 hiç gelmese ama onu yerine iki farklı şekilde 2+1 gelse yüzlerin toplamı yine iki farklı şekilde 3 edebilir. Birinci zarımızda 2 ile numaralandırılmış iki yüz olsa bu durum mümkün olabilir. Şu anda ilk zarımızın ilk üç yüzünü 1 – 2 – 2 şeklinde yeniden numaralandırdık.
Toplamın 4 olduğu duruma bakalım. Bu durum standard zarlarda 1+3, 2+2 ve 3+1 olaylarıyla mümkün. Bu olaylar yerine ilk zarda iki farklı şekilde 3 geldiğini düşünelim. Bu yeni numaralandırmayla ilk zarmımız yeniden yazalım, 1 – 2 – 2 – 3 – 3. Bu arada yeni ilk zardan 1, ikniciden 3 gelebileceği durumu da unutmayalım. Yani yeni zarlarda 4 toplamını veren üç olay var 3 + 1, 3 + 1, 1 + 3. Bu durumda ikinci zarda 2 olmaması lazım, yoksa 2 + 2 gelebilir. Dağılım bozulur!
Gelelim toplamın 5 olduğu duruma. Standard zarlarda sadece 1 + 4, 2 + 3, 3 + 2, 4 + 1 olayları bu toplamı veriyordu. Yeni zarlarda 2 + 3, 2 + 3 olayları toplam 5 veriyor. Toplamı 5 edecek iki olaya daha ihtiyacımız var. İlk zarımızın yeniden numaralanmamış son yüzünü 4 ile numaralandıralım. Yani yeni birinci zarımız 1 – 2 – 2 – 3 – 3 – 4 oldu. Bu durumda 4 + 1 olayı da toplamda 5 veriyor. Geriye 5 vermesi gereken bir olay kaldı. Bunu bulmak için ikinci zarımızın üçüncü yüzünü 4 ile numaralandıralım, yani bu zarın ilk üç yüzü 1-3-4 oldu. Son olay da 1 + 4 olarak geldi, ve toplam 5 eden yine dört tane olay var. Dağılım değişmedi.
Toplam 6 durumu: İlk zarımızı artık bulduk, 1 – 2 – 2 – 3 – 3 – 4. İkinci zarı da kısmen numaralandırdık: 1-3-4. Bu zarlarla 2 + 4, 2 + 4, 3 + 3, 3 + 3 olayları 6 ediyor. Bir olay daha lazım 6 eden. İkinci zarın bir yüzünü de 5 ile numaralandıralım: 1-3-4-5. Bu durumda bir 1 + 5 olayı da 6 verir.
Toplam 7 durumu: Mevcut zarlarımızla 2 + 5, 2 + 5, 3 + 4, 3 + 4, 4 + 3 olayları toplamda 7 ediyor. 7 etmesi gereken bir olaya daha ihtiyaç var. İkinci zarın yüzlerinden birini de 6 ile numaralandıralım: 1-3-4-5-6. Son olarak 1 + 6 olayı da 7 verir.
Elimizdeki yeni zarlarla toplamı 8 eden beş farklı olay olduğunu görmek kolay. Gelelim toplamın 9 olduğu durumlara. 3 + 6, 3 + 6, 4 +5 olayları toplamda 9 ediyor. Bu toplamı veren bir olay daha lazım. İkinci zarın açıkta kalan son yüzünü 8 ile numaralandırırsak bir de 1 + 8 olayı toplam da 9 edecek.
Bu aşamada iki tane yeni zar elde ettik. 1 – 2 – 2 – 3 – 3 – 4 ve 1 – 3 – 4 – 5 – 6 – 8.
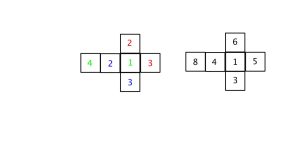
Geriye kalan toplamların da standard zarlarla aynı sıklıkta geldiğini göstermek artık kolay! Sizlere bırakıyorum.
Kaynaklar
1) Antonick, G. “Col. George Sicherman’s Dice”, Wordplay, The crossword blog of New York Times, http://wordplay.blogs.nytimes.com/2014/06/16/dice-3/ erişim tarihi: 01/07/2014.
2) Gardner, M. “Mathematical Games”, Scientific American 238 (2): 19–32. 1977
3) Wikipedia “Sicherman Dice”, Wikipedia, The Free Encyclopedia,
http://en.wikipedia.org/wiki/Sicherman_dice, erişim tarihi: 01/07/2014.


Yorum Ekle