SÜRÜLERİN VE KALABALIKLARIN HAREKETİ

İki üç yıl önce bir hafta sonu Beyoğlu’nda dolaşmaya çıkmıştım. Akşamüstü İstiklâl’den Taksim’e doğru yürüyor, bir yandan da aylak aylak etrafa bakınıyordum. (Taksim’de sıkıyönetimin olmadığı zamanlardı ve kafamıza nereden gaz kapsülü gelir diye dikkat etmemiz gerekmiyordu.)

Meydana ulaştığımda gökyüzünde kalabalık bir kuş sürüsü gördüm. Şehirde alıştığımız martı veya serçe sürüleri gibi değildi. İzlenimci bir ressamın kara noktalarla çizdiği, bilinçli dev bir varlık gibi görünüyordu, mavilikte bir damla misali sağa sola yalpalanıyordu. Maksem’in duvarına yaslanıp seyre daldım. Ara sıra sürüden bir grup kopuyor, ardından tekrar birleşiyordu. Sürü dalgalanıyor, titreşiyor, spiral kollar uzatıyor, sonra yine topaklanıyordu. Grup bir bütün olarak aniden yön değiştirse de, hiç bir kuşun sürünün dışında kaldığı görülmüyordu. Yüzlerce, belki binlerce kuşun büyüleyici dansı gün batana kadar sürdü.

Sığırcık sürülerinin sihirli uçuşlarını dünyanın birçok yerinde görmek mümkün. “Starling murmuration” kelimeleriyle yapılacak bir arama size pek çok resim ve video gösterecektir. Özellikle açık arazilerde çekilen videolar hayranlık uyandırıcı.

Sadece sığırcıkların değil, pek çok hayvan türünün sürü halinde hareket ettiğini biliyoruz: Birçok kuşun yanı sıra balıklar, bizonlar, zebralar, çekirgeler, kurtlar, insanlar, hatta bakteriler bile sürü davranışı sergilerler. Omurgalı veya omurgasız, memeli veya yumurtlayan, sıcakkanlı veya soğukkanlı, bu kadar farklı canlıda görülen bu temel davranış, sürüleşmenin çok önemli bir evrimsel avantaj sağladığını gösteriyor.

(Sol üst: Walwyn – Flickr. Sağ üst: Joan Campderrós-i-Canas – Flickr. Sol alt: Wikimedia Commons. Sağ alt: Tambako The Jaguar – Flickr)

Neden sürüler oluşur?

Sürü halinde toplu hareket etmenin en büyük faydası korunma sağlaması. Sürünün kenarında değilseniz dışarıdan yaklaşan bir avcı sizin için tehlike oluşturmaz. Kenardaki azınlık da hep dışarıda kalmaz zaten, içeriye doğru girerler. Avcı bazen sürüye yaklaşamaz bile; sürünün bir üyesi bile avcıyı tespit etse diğerlerine haber verir ve kaçmalarını sağlar. Avcı peşlerinden koşsa bile, hangi birini yakalayacağını şaşırıp zaman kaybeder.

Yırtıcı hayvanların çoğu yalnız avcılardır, ama kurtlar ve aslanlar gibi sürü halinde avlanan türler de vardır. Böylece büyük avlara hep beraber saldırabilirler. Sürüleşme daha kurnazca amaçlarla da kullanılabilir. Mesela, bir sırtlan çetesi bir çitanın üstüne yürüyüp, alnının teriyle avladığı antilopu bırakıp gitmeye zorlayabilir.

Sürüleşmenin daha çılgınca sebepleri de olabiliyor. Meselâ çöl çekirgelerinin kıtlıkta birbirlerini yedikleri bilinir. Ergen çöl çekirgeleri daha yetişkin olmadıkları için uçamazlar ama yürüyebilirler. Grup belli bir kalabalığa ulaştığında yamyamlık belirtileri başlar. Sübyan çekirgeler arkalarındaki arkadaşlarının “ittirmesini” hissettiklerinde, yem olmamak için sürekli ileri doğru yürürler. Birbirlerine çok yaklaşmaktan da kaçındıkları için sağa sola sapmadan dümdüz giderler. Böylece milyonlarca bireylik bir sürü oluşur, ama birbirlerine sokulmak istediklerinden değil, tersine, kaçınmak istediklerinden.

Başka bir örnek olarak, Amazon tırtıl katarlarının garip hareketini daha önce Açık Bilim’de işlemiştik.

Her türün sürüleşmesi farklı farklı. Türün hareket kabiliyetine, kıvraklığına, algı gücüne, beyin kapasitesine ve çevre şartlarına göre çok farklı sürü davranışları görülebiliyor. Bazılarında hayvanlar omuz omuza ilerlerken, bazılarında gevşek bir etkileşim oluyor. Bazılarının bariz bir lideri var (mesela yaban kazları), bazı türlerde ise yok (mesela sığırcıklar), bazılarında ise bireyler hiyerarşideki yerlerine orantılı olarak takip ediliyorlar (mesela inekler).

Hesaplama modelleri ve simülasyonlar

Sürü hareketinin nasıl oluştuğunu anlamanın yollarından biri, “birey temelli modelleme” uygulamak. Bu yöntemde sürüdeki her bir hayvanın (sığırcık, balık, zebra) belli basit kurallara uyarak kendi başına hareket ettiği varsayılır. Bireyler hareketlerini yakın çevrelerine bakarak ayarlarlar. Bu tür bir modelde koordine edici bir lidere ihtiyaç yoktur.

1987’de bilgisayar grafiği uzmanı Craig Reynolds böyle bir model kurdu. Reynolds’un bilgisayarında yarattığı “kuşumsu”lar sabit hızda uçuyorlar, en yakın komşularına göre uçuş yönlerini şu üç basit kurala uyarak an be an düzenliyorlar:

1. Ayrışma: Fazla yakın komşulardan uzaklaş.
2. Hizalanma: Komşuların gittiği yönlere bak, ortalama yöne göre kendini hizala.
3. Birleşme: Komşuların orta noktasına yönel.

Elbette bu kuralların her biri ayrı yönlere götürebilir. O zaman “kuşumsu” üç yönün vektör toplamını alarak kendini ayarlar.

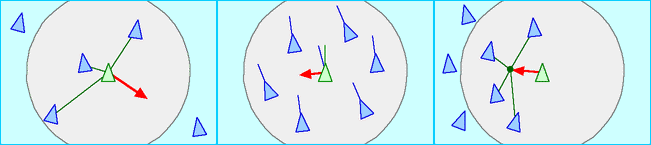
Reynolds bilgisayarını bu kurallarla programladığında gerçek kuşlara benzeyen bir sürü hareketi oluştuğunu gördü:

Reynolds modeli, sadece yakın komşular arası etkileşmelerle, sürü ölçeğinde düzenli bir hareketin ortaya çıkabileceğini gösterdi. Kuşumsuların hareketi bireyseldir; bütün sürüyü yöneten kimse yoktur. Ama her bireyin kendi komşularına göre kendini ayarlaması, ufak bir değişimin bile hızlıca sürü çapında dalga dalga yayılması anlamına gelir. Her şeyi yöneten bir merkez olsaydı, iletişimdeki gecikmeler yüzünden bu kadar hızlı tepki vermek ve düzen sağlamak mümkün olmazdı. Yani, sığırcıkların büyüleyici dansı için bir liderin gerekli olmasını bırakın, liderin hiç olmaması gerekiyor. Merkezi yönetimin bulunmaması, hızlı uyum ve kıvraklık sağlıyor.

Reynolds’un öncülük ettiği birey temelli simülasyon yaklaşımı, sağladığı gerçekçilik nedeniyle daha sonra animasyon filmlerde ve oyunlarda kullanıldı. Örneğin, 1994 tarihli Aslan Kral filmindeki yaban sığırı koşuşması sahnesi, böyle bir algoritmayla hazırlandı.

https://www.youtube.com/watch?v=2m-42ek85G4

Modeller ne kadar gerçekçi?

Sürü hareketi (veya daha genel bir ifadeyle “toplu hareket”) ile sadece biyologlar ilgilenmiyor. Fizikçiler ve matematikçiler Reynolds’un varsayımları üzerinde çeşitlemeler yaparak bilgisayarlarında sürüler yaratıyorlar, ve bireysel davranış kurallarının bütün sürünün hareketini nasıl etkilediğini inceliyorlar.

Bu tür modellerin eksik tarafı, alışıldık anlamda bilimsel kesinlik sağlamamaları. Bir astronom Newton yasalarını, bir meteorolog akışkan dinamiği denklemlerini bilgisayarında işleyerek geleceği (meselâ Ay tutulmalarını veya yarınki havayı) hassas bir şekilde tahmin edebilir. Henüz gerçekleşmemiş şeyleri tahmin edebilmek, bir bilimsel teorinin en önemli güçlerinden biridir.

Ancak sürüler gibi karmaşık sistemlerde henüz bu güce sahip matematiksel teorilerimiz yok. Kullanılan birkaç değişik model var, ve bu modeller sadece akla yakın bazı varsayımlardan ibaret. Örneğin, bu alanın en önde gelen araştırmacılarından Tamas Vicsek’in adıyla anılan Standart Vicsek Modeli, Reynolds modelinden bile basittir: Her sanal kuşun gideceği yön, kendisine belli bir mesafede bulunan kuşların ortalaması olan yön olarak belirlenir. Ek olarak, bu yönde küçük ve rastgele bir değişiklik de yapılır. Bu rastgele değişiklik (“parazit”) bir sürü iç ve dış faktörü içinde barındıran bir torba gibidir: Havanın puslu olması, kuşun bilgi işlemesindeki hatalar, hava akımları gibi ayrı ayrı eklemenin çok zor olacağı faktörler rastgelelikle temsil edilirler.

Sürü modellerinin çoğu basit ve sade varsayımlara dayanırlar, bu açıdan gerçekçi değildirler. Meselâ modellerdeki sanal kuşlar birer “nokta”dır. Ne vücut biçimleri, ne kanat uzunlukları, ne de zihin kapasiteleri hesaba katılmıştır. Oysa ki bu ayrıntılar kuşların kıvraklıklarını, güçlerini, algı hızlarını çok değiştirir. Bu ayrıntıların bir kenara bırakılması yüzünden de, bilgisayarda yaptığımız hesabın sonucunun kuşları gözleyerek elde ettiğimiz verilere tam uymasını bekleyemeyiz.

Bu sebeple, karmaşık sistem modellerinin anlayışımıza yaptığı katkı daha çok niteliklere dairdir. Modeli nasıl ayarlamalı ki kuşlar birbirine çarpmasın? Sürünün bir arada uçması için kuşların ne kadar yakın olması gerek? Sürü bölünüp birleşebiliyor mu? Kuşların tahmin hataları sürünün oluşumunu etkiliyor mu? Bu tür soruların cevapları, sayısal doğruluktan çok, “benzerlik” olarak verilir. Modeller en fazla, hangi varsayımların belli olguları ortaya çıkarmak için yeterli olduğunu söyleyebilirler.

Belki ileride Newton yasaları veya Navier-Stokes denklemleri gibi doğruluk payı çok yüksek modeller kurulabilecek, ama şimdilik elimizdeki matematiksel yöntemler karmaşık sistemleri hem sade hem de isabetli olarak tarif etmeye yetmiyor.

Bununla beraber modeller bazen sadece matematiksel özelliklerinin ilginçliği için de incelenirler. Sözgelişi, Vicsek’in modellerindeki “parazit” (kuşumsuların yönlerine eklenen rastgele bileşen) belli bir seviyenin altına indiğinde sürünün bireylerinin kolaylıkla birbiriyle hizalandığı, çok parazitli bir ortamda ise dağınık kaldıklarını görüyoruz. Bu gözlem, fizikte “faz geçişleri” olarak adlandırılan olguya matematiksel olarak denk özellikler gösteriyor. Bu tür modellerin birikmesiyle önümüzdeki yıllarda kendi gücüyle hareket eden nesnelerin (yani canlıların) fiziksel hareket denklemlerinin keşfedilmesi mümkün olabilir.

Gözlemler

Teorik modellerin yanı sıra, gözlem yoluyla sürü hareketine dair veriler de toplanıyor. Ama bu tür veri toplama epey zor, çünkü haliyle kontrollü deneye pek imkân vermiyor. Deneyci sürüye fazla yaklaşırsa, sürünün davranışını bozma riski de var.

Yine de teknolojiyi akıllıca kullanarak bu zorluklar aşılabiliyor. İtalyan fizikçi Michele Ballerini ve çalışma arkadaşları, üç ayrı konuma yerleştirdikleri kameralarla sığırcık sürülerini filme almışlar. Benzer çalışmalarda on-yirmi bireylik sürüler takip edilebilmişken, bu çalışmada 2700 bireye varan sürüler incelenmiş. Farklı açılardan kayıt alındığı için, ileri görüntü işleme teknikleri kullanarak tek tek kuşların üç boyutlu hareketini tekrar üretmeleri mümkün olmuş. Bu sayede, modellerin test edilebileceği çok önemli bir veri bankası oluşturabilmişler.

Veriler yeni bilgiler sağlamış. Sözgelişi, sığırcık sürüsünün pide gibi yayvan bir yapıda olduğu görülmüş; yani sürünün düşey yöndeki genişliği, yatay yönlerdekinden çok daha az. Bu, mevcut sanal kuş modellerinin yakalayamadığı bir özellik. Sebebi ise basit: Yukarı aşağı hareket etmek, yatay hareketten daha fazla enerji harcatıyor. Yerçekimine karşı çaba göstermek düşey yöndeki kıvraklığı azaltıyor.

Modeller, kuşların belli bir mesafeye kadar olan komşularına göre hizalandıklarını varsayıyor. Verilere göre, kuşlar birbirine çok yakın uçuyorsa bu varsayım doğru. Sürülerde her bir kuşun kanat açıklığı doğal bir mesafe ölçüsü sağlıyor, ve kuşlar gerçekten de çok yakındaki komşularından uzaklaşıyorlar. Ancak çarpışma tehlikesi yoksa, kuşlar yönlerini belirlemek için komşularına bakarken uzaklık bir önem taşımıyor. Her bir kuş çevresindeki altı veya yedi yakın komşusuna göre hizalanıyor. Bu da modellerde bulunmayan bir özellik.

Sürülerin kamerayla gözlemlenmesi, kayıtların dijital veriye dönüştürülmesi, ve matematiksel olarak incelenmesi henüz yeni bir alan. Bu incelemeler sonucunda toplu harekete dair birçok yeni ve ilginç özellik keşfediliyor ve bu davranışların açıklanması için matematik ve fiziğe başvurmak gerekiyor. Bu konuda araştırma yapmak isteyenleri bekleyen pek çok cevapsız soru mevcut.

İnsan dinamiği

İnsanların grup halindeki davranışı da aynı bağlamda, gerek modeller kurarak gerek gözlemler yaparak inceleniyor. İnsanların grup halinde nasıl hareket ettiğini anlamanın uygulama alanları daha fazla. Sözgelişi, binaların inşa planında sıkışmadan yürünebilecek bir düzen kurmak, panik halindeki insanların güvenli ve hızlı bir şekilde dışarı çıkmasını sağlamak gibi önemli uygulamaları var.

İnsanlar normal şartlarda kuşlar veya balıklar gibi sürü oluşturmasalar da, yine de birbirinden kaçınma davranışı, ve (özellikle panik halindeyken) diğerleriyle aynı yöne gitme davranışı gösteriyorlar. İnsanların yürüme davranışına dair matematiksel modeller, bireyler arasındaki uzaklığa bağlı olan “sosyal kuvvetler” denen sanal itme-çekme kuvvetlerini kullanıyor. Bu modellerin parametreleri video kayıtlarından elde edilen deneysel verilere göre ayarlanınca, epeyce gerçekçi bir matematiksel model elde edilebiliyor.

Kalabalık bir metro koridorunda veya tıklım tıklım bir sokak pazarında yürüdüyseniz, karşılıklı iki yönden gelen insanların kendiliklerinden belli bir düzene girdiğini, araç trafiğindeki gibi şeritler oluşturduğunu farketmişsinizdir. Yayalar karşıdan gelenlere çarpmamak için kenara çekile çekile, en sonunda gittikleri yönde arka arkaya dizilirler. Bu düzen oluşunca artık yer değiştirmeleri gerekmediği için bu şeritler istikrarlı olarak devam eder. Tabii kendi kendine oluşan bu şeritler, caddelerdeki gibi bir gidiş bir geliş düzeninde olmuyor, yön değiştirerek yanyana bulunan birkaç gidiş birkaç geliş şeridi olabiliyor.  Sosyal kuvvetlere dayalı bilgisayar simülasyonları bu gözlenen olguyu başarıyla tekrar yaratabiliyor.

Panik durumu ise bambaşka dinamiklere yol açabiliyor. Sözgelişi, tek kapısı bulunan bir salonda yangın çıktığında herkes paniğe kapılarak çıkışa koşturuyor. “Sosyal kuvvet” modelleri böyle bir senaryoda grubun kapıda sıkışıp kalacağını, hareket kabiliyetinin azalacağını öngörüyor. İlginç nokta şu: Bireyler daha yavaş hareket ettiklerinde düzgün ve hızlı bir şekilde dışarı çıkabiliyorken, aceleyle koşturduklarında çıkışları çok yavaşlıyor.

İnsanları bir atom gibi, bir grubu da bir gaz gibi düşünürsek, insanların hareket hızı kabaca gazın “sıcaklığı”na denk gelir. Bu davranıştaki ilginçlik, gazı ısıttığımızda “katılaşması”, yani insanların hareket edemez duruma gelmesi. Sıkışmayı engellemek için, yoğunluğun azalması lâzım. Yani simülasyonlar sağduyumuzu teyit ediyor: Tehlike durumunda koşmamak lâzım.

Ancak paniğe kapılan insanlar bu sağduyuyu gösteremeyebilir. O zaman bina tasarımında bazı numaralar (bilgisayarcı deyimiyle “hack”ler) kullanmak gerekebilir. Sözgelişi, delice gözükse bile, çıkış kapısına yakın bir sütun koymanın, salondan çıkışı hızlandırabildiği görülmüş. Kalabalık sütunun çevresinde birikiyor, bu da kişiler arasındaki basıncı daha geniş bir alana yayıyor. Sütunun etrafından dolanmaya mecbur kalmak, telaşlı kalabalığın salonu boşaltma hızını artırıyor. Garip ama gerçek.

Bu simülasyonları deneysel olarak test edemiyoruz, çünkü acil durum tahliyesiyle ilgili konularda kontrollü deneyler yapmak etik değil. İnsanları farlı salonlara koyup yalandan panik yaratamazsınız. Avustralyalı araştırmacı Majid Sarvi bu sorunun üstesinden gelmek için karınca sürüleriyle deneyle tasarlamış. Karıncaları dar bir kapısı bulunan yapıların içine koymuş ve ne kadar çabuk tahliye ettiklerini ölçmüş. Karıncaların çıkışlar köşelere yakın olduğunda hızlıca çıktıklarını, duvarın ortasındaki kapılarda ise yuarıdaki resimdeki gibi biriktiklerini görmüş. Bu gözlemini simülasyonlarla insan hareketi modelinde denediğinde yine yüksek bir verimlilik gözlemiş. Ama karıncaların davranışı insanlarınkinden çok farklı olduğu için bu deneylerin ne kadar faydalı olacağı tartışılır.

Bina tasarımında yaya trafiğini artırmak için ilk bakışta makul görünen ama işe yaramayan “hack”ler de var. Meselâ, dar bir koridorda insanların yürüyüşünü hızlandırmak için araya geniş bölgeler koymanın, hızlandırmak bir yana, yürüyüşü yavaşlattığı simülasyonlarla gözlenmiş. Sebebi basit: Yürürken araya mesafe koymak isteyen insanlar geniş bölgeye geldiklerinde kenarlara yayılıyorlar, ancak dar bölgeye gelince tekrar hizalanmak için yavaşlamak ve diğerlerini de yavaşlatmak zorunda kalıyorlar.

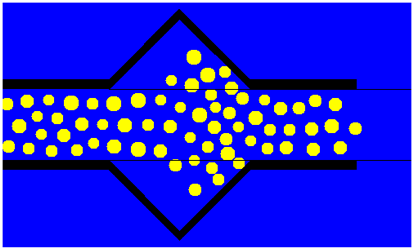
Aynı etkiyi araç trafiğinde de görebilirsiniz. Otoyol gişelerinin hemen sonrasında trafik çok yoğun olur, oysa ki yola giren yeni araç yoktur, nereden çıkar bu yoğunluk? Üç şeritli bir otoyolda düzenli bir hızda giden araçlar, gişelere gelindiğinde altı şeride yayılıp, gişelerden sonra tekrar eski düzene girmek için birbirlerinin önünü keserler, trafik bu yüzden yavaşlar.

Podcast: Play in new window | Download

Subscribe: RSS

Kaynaklar

• Tamás Vicsek, Anna Zafeiris. Collective Motion. Physics Reports, Vol. 517, pp. 71-140, 2012
• Craig Reynolds, Boids. Erişim: 3.6.2014
• Carl Zimmer, From Ants to People, an Instinct to Swarm. The New York Times, 13 Kasım 2007.
• Ballerini vd., Empirical investigation of starling flocks: a benchmark study in collective animal behavior. Animal Behaviour, vol. 76, sayı 1, Temmuz 2008, sayfa 201–215.
• Dirk Helbing, Anders Johansson.  Pedestrian, Crowd, and Evacuation Dynamics. arXiv:1309.1609 [physics.soc-ph]
• OpenABM, Escape Dynamics. Erişim: 3.6.2014
• Paul Marks, Panicky ants help design safest exit strategy. New Scientist, 4.6.2013.