YAŞAMA VE ÖLÜME İSTATİSTİKSEL BİR BAKIŞ

Yaşam ve ölüm, insanlık kendini bildi bileli belki de en çok konuşulan ve yorumlanan iki konu oldu. Üzerine yazılan onbinlerce sayfalık edebiyat bir kenara, yaşam ve ölüm bilimin de anlayıp çözmeye çalıştığı en büyük sırlardan. Tek hücreli canlılarla başlayan hayat tahminen 3,6 milyar yıllık evrim sonucunda inanılmaz bir çeşitlilikle birlikte bugünkü haline ulaştı. Evrime paralel olarak, organizmaların yapıtaşları olan hücreler ve onların yaşam döngüleri de karmaşıklaştı. Canlılar dünyasının en yeni üyeleri olan ve içine dahil olduğumuz memeliler ise biyolojik açıdan en karmaşık yapıya sahiptir desek herhalde yanlış dememiş oluruz. Bununla birlikte, karmaşık canlıların büyük bir kısmı için yaşamın temel prensipleri basit ve sabit; canlılar doğar, büyür ve ölür. Mikro ölçekte hücrelerin, alışageldiğimiz makro ölçekte ise organizmanın ölümü doğadaki yaşam döngüsünün bir parçasıdır.

Hücrelerin ve de genel olarak canlıların yaşam döngüsünde iç etmenler kadar dış etmenler de çok önemli bir rol oynuyor. İç etmenlere örnek olarak ebeveynlerden alınan genetik miras ve bunun ürünü olan hücre ve organizma yapısı verilebilir. Dış etmenler ise tahmin edeceğiniz gibi çevresel koşullar ve diğer canlılarla olan etkileşimlerdir. Son birkaç bin yıldır yaşam müsabakasında diğer memelilere ve birçok karmaşık canlıya kıyasla insanlar oldukça önde, en azından hızla ön sıralara doğru ilerliyorlar. Teknoloji ve tıbbın soluksuz ilerlemesiyle birçok hastalığın ya önü kesildi ya da tedavisi bulundu. Yaşam koşulları iyilestirildi ve en elverişsiz ortamlarda bile uygun yaşama koşulları oluşturuldu. Ortalama insan ömrü taş devrinde 30 civarında iken günümüzdeki dünya ortalaması 70’e merdiven dayadı [1]. Gelişmiş ülkelerde bu rakam en az 10 yaş daha yüksek. 3 basamaklı yaşlar bile artık kulağa alışık geliyor. Haliyle dünya nüfusu da yerinde durmadı, katlanarak arttı ve hâlâ artıyor.

Bizim için değişen ve gelişen bu kadar şeye rağmen, yukarıda bahsettiğimiz yaşam döngüsü aralıksız işlemeye devam ediyor. Yani yaşlanma ve ölüm hâlâ kaçınılmaz. İşin ilginç kısmı ise, bu süreçlerin insan hayatını etkileyen bu kadar faktöre rağmen nüfus ölçeğinde formüle edilebilen,  kararlı istatistiksel davranışlar sergilemesi. Bu makalede size yakamızı bırakmayan işte bu matematiksel bağıntıdan bahsedeceğim. İnsanlar için yaşam kendi içinde ne kadar karmaşık da olsa, görünüşe göre gerçekler tek bir formüle kadar indirgenebiliyor.

Veriler ve grafikler hakkında

Makaledeki tahliller için 3 bölgeye ait nüfus verileri kullanıldı. Bunlar 2013 yılı Türkiye [2], 2009 yılı ABD [3]  ve 2010 yılı AB-16 ülkelerine* [4] ait nüfus ve ölüm verileri. Herhangi bir yaş (x) için, hayatta olan kişi sayısı H(x) ve o yaşta ölen kişi sayısı Ö(x) göz önüne alınarak aşağıdaki hesaplamalar yapıldı:

-x yaşındaki insanlar için ölüm oranı: Ö(x) / [Ö(x)+H(x)] (Resim 1)

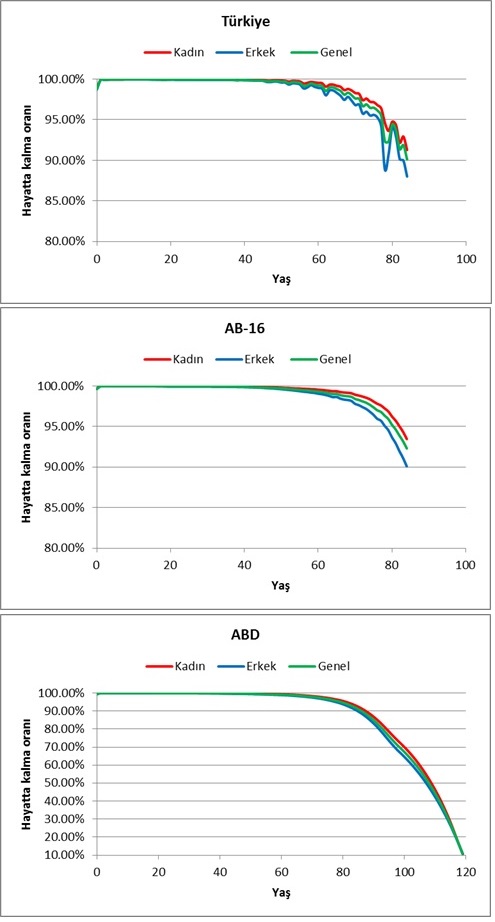
-x yaşındaki insanlar için hayatta kalma oranı: H(x) / [Ö(x)+H(x)] (Resim 2)

-x yaşındaki insanlar için 8 yıl öncesine kıyasla ölüm oranı: Ö(x) / Ö(x-8) (Resim 3)

Bu hesaplamalar kadın, erkek ve genel nüfus için tekrarlandı. Mevcut veriler Türkiye ve AB-16 için 84. yaşa kadarken, ABD için 120. yaşa kadar bulundu. Grafikler yazar tarafından Açık Bilim için hazırlandı.

Gompertz ve çift üstel bağıntısı

Resim 1’de belli bir yaştaki insanlar için ölüm oranları gösteriliyor. Mesela, 40 yaşındaki insanlar arasında ölüm oranı Türkiye nüfusu için binde bir civarında. Türkiye, AB-16 ve ABD nüfuslarındaki ölüm oranlarını birbirleriyle karşılaştırırsanız nüfusların çok benzer davranışlara sahip olduklarını görürsünüz:

-Doğumdan 12. yaşa kadar azalan bir ölüm oranı var. Burada bebek ve çocuk ölümlerindeki göreceli sıklık ortada. Tahminen çocukların halen gelişmekte olan bağışıklık sistemleri burada baş rolü oynuyor.

-Ortalama 25. yaştan sonra ivmeli bir şekilde artan bir ölüm oranı var. Bu oran 60. yaşa kadar %1’i geçmiyor. ABD verilerinden gördüğümüz gibi 90 yaş civarında ivmede bir yumuşama söz konusu.

-İncelenen üç nüfusta da erkeklerdeki ölüm oranı kadınlardaki ölüm oranından daha yüksek, ortalama olarak 2 kat. ABD nüfus verilerine göre ancak 100 yaşından sonra erkekler ve kadınlar arasındaki bu fark ortadan kalkmış.

-ABD’ye ait grafik gösteriyor ki, 120 yaşına gelmiş bir kişinin sonraki yıl içinde ölme ihtimali %90’dan fazla.

Ölüm oranı ve hayatta kalma oranı birbirini tamamlayan iki rakam olduğuna göre durumu bir de tersten inceleyelim. İnternette okuduğum bir popüler bilim makalesinde, nüfus bazında hayatta kalma olasılığının yaşa bağlı olarak kurallı bir şekilde azaldığı yazıyordu [5]. Daha detaylı anlatmak gerekirse, 1825 yılında İngiliz matematikçi Benjamin Gompertz’in geliştirdiği bir demografik (yani insan nüfusunu istatistiksel olarak inceleyen) model ile belli bir yaştaki insanın hayatta kalma olasılığı gayet yüksek bir başarıyla hesaplanabiliyor [6,7]:

Burada P(x), x yaşındaki insanlar için hayatta kalma olasılığını ve e meşhur Euler sayısını (2,71828…) temsil ediyor. Denklemin değişebilen parametreleri ise a, b ve c. 25 rakamı ise bu denklemin 25 yaşından itibaren geçerli olduğunu söylüyor. Sebebi ise yukarıda belirttiğimiz gibi, insan nüfusunun 25 yaşından itibaren bu kararlı davranışı sergilemesi. Resim 2’deki grafiklerde belli bir yaştaki insanlar için hayatta kalma oranları gösteriliyor. Bu grafiklerdeki veriler, yukarıda verdiğim Gompertz bağıntısıyla oldukça güzel örtüşüyor.**

Buradaki en önemli nokta Gompertz denkleminin çift üstel bir bağıntıdan oluşması. Sıradan bir üstel bağıntıya kıyasla çok daha hızlı azalan değerlere sahip bu denklem sadece yaşlanan nüfus davranışını değil, insanların ulaşabileceği azami ömrü de oldukça mantıklı bir çerçevede tahmin ediyor. Şöyle ki, eğer Gompertz bağıntısı yerine tek üstel bağıntı içeren bir model kullansaydık, modele göre 300 yaşını geçen insanlar görmemiz gerekirdi [8]. Kayıtlara geçmiş en yaşlı insan ise 1997 yılında 122 yaşında ölen Jeanne Calment [9]. Gompertz’in modeliyle bir hesaplama yaparsak 122 yaşında birinin Türkiye’deyse %0,01, AB-16 bölgesindeyse %1,5, ABD’de ise %5,5 olasılıkla o yıl hayatta kalabileceğini buluruz.***

8 yıl sonra

Yaşla birlikte katlanarak artan ölüm oranını karşılaştırmalı incelersek Resim 3’deki gibi bir tabloyla karşılaşıyoruz. Burada, belli bir yaştaki insanlar için ölüm oranı, kendilerinden 8 yaş daha genç insanlara ait ölüm oranıyla kıyaslanıyor (mesela 30 yaşındaki ölüm oranı / 22 yaşındaki ölüm oranı). Dolayısıyla grafik ancak 8. yaşta başlıyor. İlk farkedilen şey AB-16 ve ABD nüfusları için 20 yaş civarındaki sert tepe noktası. ABD nüfusunda 20 yaşındaki ölüm olanı 12 yaşındakine kıyasla erkekler için 10, kadınlar içinse 4 kat daha fazla. Peki niye bu kadar yüksek bir artış var veya niye kadın ve erkeklerin durumu bu kadar farklı gibisinden sorular aklımıza geliyor olabilir. Oldukça göze batan bu durum için açıklama yapmaktan özellikle kaçınıyorum, çünkü bu ayrıca araştırma gerektiren bir yazı konusu. Şu noktada unutulmaması gereken şey ölüm oranı değerlerine tek tek değil, birbirlerine oranlayarak bakıyor olmamız. Aslında bellı bir yaştaki ölüm oranı 60 yaşından önce %1’e ulaşmıyor bile. İlginç bir durum ise Türkiye nüfusuna ait verilerde böyle bir tepe noktasının yer almaması.

20 yaş civarındaki tepe noktasını bir kenara bırakırsak, 30 yaşından itibaren orantısal ölüm oranı her nüfus için oldukça kararlı bir tablo sergiliyor. Bir başka deyişle, yaşa bağlı ölüm oranı 30 yaşından itibaren neredeyse her 8 yılda bir ikiye katlanıyor. Üstelik kadın ve erkek nüfus arasındaki fark da yok denecek kadar azalıyor.  Peki neden 8 yıl? Bu soruya cevap vermek oldukça zor. Öne sürülen modellerden birisi vücudun gittikçe zayıflayan bağışıklık sistemi üzerine kurulu [9]. Bu modele göre, yaşla birlikte doğrusal olarak zayıflayan bir bağışıklık sistemi yüzünden vücudun hayatta kalma mücadelesini kaybetme riski üstel olarak artıyor. Tabi burada iç etmenler kadar dış etmenler de büyük bir rol oynuyor. Bir veya iki asır öncesine ait nüfus verileri incelenebilseydi, belli bir yaştaki ölüm oranının belki 8 yerine 6 yılda bir ikiye katlandığını görecektik. Çünkü bundan 100 ya da 200 yıl önceki yaşam koşullarının şu andakinden daha elverişsiz olduğu aşikar. O zaman, ilerleyen tıp ve yaşam standartları ile gelecekte bu rakam belki 8 değil de 10 olabilir. Tabii bunların hepsi tahmin. Kesin olan bir şey var ki, biyolojik saatimiz her durumda hızlanarak çalışmaya devam ediyor.

Sonuç

Gördüğünüz gibi insan nüfusu yaşlanma ve ölüm konusunda dünyanın farklı yerlerinde bile olsa oldukça benzer davranışlar sergiliyor. Ölüm olasılığının yaşla birlikte ivmelenerek arttığı ve 120 yaş civarının azami sınır olduğu bu senaryoyu üstelik tek bir formüle dökebiliyoruz. İşin teorik yanı bir tarafa, tabii ki bazı fiziksel, daha doğrusu biyolojik temeller bu sonuçları doğurmak zorunda. Yazının başında evrimle birlikte canlıların biyolojik açıdan gelişip karmaşıklaştığından bahsettik. Görünüşe göre bu sürecin sonuçlarından birisi de canlıların yaşlanıp ölmesi. Evrimin devamlılığı ve canlıların kendilerini geliştirebilmesi için de aslında bu durum oldukça önemli.

Bizim için kabul etmesi ne kadar güç de olsa, hücrelerimiz sonsuza kadar yaşamaya veya bölünmeye programlı değil. Mesela, hücre bölünmesinde anahtar rol oynayan telomer denen ipçikler her hücre bölünmesi sonrasında biraz daha kısalıyor. Hayflick sınırı olarak tanımlanan, 40-60 bölünme sonrasında ise hücrelerimiz daha fazla bölünemez, dolayısıyla vücudumuz da kendini yenileyemez hale geliyor [10]. Bizim için durum buyken, doğada yaşlanmayan daha doğrusu yaşlandıkça ölüme yaklaşmayan canlılar da var [11]. Kimbilir, belki bu canlılar bize daimi gençliğin sırrını gösterebilir. Bu sırrı gerçekten kullanabilir miyiz ve yerküre ölümsüz bir insan nüfusunu kaldırabilir mi bu da başka bir makalenin konusu.

*AB-16 ülkeleri: Almanya, Avusturya, Belçika, Finlandiya, Fransa, Hollanda, İrlanda, İspanya, İtalya, Güney Kıbrıs Rum Yönetimi, Lüksemburg, Malta, Portekiz, Slovenya ve Yunanistan.

**Resim 2’deki veriler için hesaplanan denklemlerin parametreleri ve hata payları. Denklemler 25-80 yaş arası için geçerlidir. (R²: Denklemin doğruluğunun ölçüsü)

*** Tabloda yer alan, bölgelere ait parametre setlerini kullanıp, Gompertz denklemine x=122 değerini verirseniz bu sonuçları bulursunuz. Unutulmaması gereken, bu parametre setlerinin 25-80 yaş aralığı için hesaplanmış olması. 122 yaş tanım dışı olduğundan hesaplanan değerdeki hata payı daha yüksek olacaktır.

Kaynaklar

Kapak resmi: http://www.flickr.com/photos/travalicando/258802176/sizes/l/

1. http://en.wikipedia.org/wiki/Life_expectancy#Life_expectancy_variation_over_time
2. http://www.turkstat.gov.tr/PreTabloArama.do?metod=search&araType=vt
3. http://www.ssa.gov/OACT/STATS/table4c6.html
4. http://epp.eurostat.ec.europa.eu/portal/page/portal/statistics/search_database
5. http://gravityandlevity.wordpress.com/2009/07/08/your-body-wasnt-built-to-last-a-lesson-from-human-mortality-rates/
6. http://en.wikipedia.org/wiki/Benjamin_Gompertz
7. http://en.wikipedia.org/wiki/Gompertz_function
8. http://arxiv.org/PS_cache/q-bio/pdf/0411/0411019v3.pdf
9. http://en.wikipedia.org/wiki/Jeanne_Calment
10. http://en.wikipedia.org/wiki/Hayflick_limit
11. http://www.nature.com/news/not-all-species-deteriorate-with-age-1.14322