Pi ($latex \pi$) için kaç basamak sayabilirsiniz? “Pi’yi üç alalım” diyenlerden misiniz, 3,14 diyen orta yolculardan mı, 3,14159 diyen mükemmeliyetçilerden mi?
Çinli kimya öğrencisi Çao Lu kadar olamazsınız. Lu, dört yıllık bir çalışmanın ardından, Pi’yi 67 890 basamağa kadar ezberlemeyi başardı. Guinness rekorlar kitabı hakemlerinin önünde Pi’yi ezberden okuması tam 24 saat 4 dakika sürdü.
Pratik amaçlar için bu derecede bir takıntıya elbette lüzum yok. Bilinen evrenin çevresini sadece bir hidrojen atomu genişliği kadar bir hatayla hesaplayabilmek için Pi’yi 39 basamağa kadar bilmek yeterli: 3,141592653589793238462643383279502884197
Ama Pi’nin bizim için değeri pratik amacının çok ötesinde. Bugün uzmanlar bilgisayarların ve algoritma teorisinin sınırlarını zorlayarak Pi’yi trilyonlarca basamağa kadar hesaplamış durumdalar. Ancak, bilgisayarların sağladığı imkânların bulunmadığı dönemlerde bile matematikçiler ve hesap meraklıları, elle hesap yaparak Pi’yi yüzlerce basamağa kadar belirlemişlerdi.
Sonsuz değişik sayı içinde, neden Pi bizim için bu kadar önemli? Neden matematikte aynı derecede yaygın olan e‘nin basamaklarını ezberlemeyi iş edinmiyoruz? Neden $latex \sqrt{3}$’ü trilyon basamağa kadar hesaplamıyoruz?
Pi’nin karizması yüksek, albenisi çok. Filmlere konu olan, romanlarda, öykülerde başrol oynayan tek sayı. Pi’nin özel önemi düşünüldüğünde bu pek şaşırtıcı değil. Dünya’ya bir uzaylı gelse belki değer verdiğimiz birçok şeyi rastgele ve anlamsız bulabilir, ama Pi hayranlığı konusunda bize hak verecektir.
14 Mart, yani 3. ayın 14. günü, bilimciler ve eğitimciler tarafından Pi günü olarak kutlanıyor. Biz de Açık Bilim’de bu kutlamaya bu yazıyla katılıyoruz. “Tüm yurtta ve dış temsilciliklerimizde törenlerle kutlandığı” günleri de görürüz belki.

Pi sayısı pratik önemi sebebiyle uygarlığın en erken dönemlerinden beri kullanılmış ilk matematik sabiti. Daire ve çemberlerle işi olan her medeniyet bu sayıyı tanımış, çeşitli yaklaşık değerler vererek kullanmış. Mısır’da MÖ 1650 yılında yazılan ünlü Rhind papirüsünde, dairenin alanının, çapın 8/9’unun karesini alınarak bulunabileceği yazılmış, ki bu Pi için 3.16049.. gibi bir değer varsayıldığı anlamına geliyor.
Mezopotamya’da ise Babil uygarlığının Pi için 3.125 gibi daha hatalı bir değer kullandığı biliniyor.
Bu yaklaşık değerler, diğer uzunluk ölçümlerinde de hassasiyet pek yüksek olmadığından, o dönemin kadastro ve inşaat işlemleri için yeterli oluyordu. Antik Yunanistan ve İyonya’daki soyut geometri tutkusu Pi’nin pratik amaçların çok ötesinde, yüksek hassasiyetle belirlenmesi isteği doğurmuş olmalı, ama Arşimet’in (MÖ 287 – MÖ 212) dönemine kadar daha doğru bir hesaplama yapılıp yapılmadığı bilinmiyor.
Arşimet’in Pi’yi hesaplamak için kullandığı yöntem, daireyi yaklaşık olarak düzgün bir çokgen kabul etmeye dayanıyor. Arşimet önce bir birim yarıçaplı bir daire aldı. Bu dairenin çevresi 2 Pi birim uzunluktadır. Köşeleri bu daireye değen bir iç altıgen çizdi. Ardından kenarları aynı daireye teğet olan, öncekinden biraz daha büyük, bir dış altıgen ekledi. Dairenin çevresi iç altıgenin çevresinden daha uzun, dış altıgenin çevresinden ise daha kısa olmalıdır. Böylece Pi için bir alt ve üst sınır elde edilir.
Arşimet, kenar sayısını artırdıkça daireye daha fazla yaklaşacağını bilerek, kenarları her seferinde ikiye bölerek altıgenleri onikigenlere, onikigenleri yirmidörtgenlere, sonra kırksekizgenlere, sonunda da doksanaltıgenlere çevirdi.

Arşimet aslında bu çokgenleri açıkça çizmedi; bunun yerine, çokgenlerin çevre uzunlukları için bir formül üretti. Birim yarıçaplı bir daireye dışarıdan değen n kenarlı bir düzgün çokgen (n-gen) çizilmiş olsun; bunun çevre uzunluğuna $latex a_n$ diyelim. Köşeleri aynı daireye içeriden değen n-genin çevre uzunluğu da $latex b_n$ olsun. Bu n-genlerin her kenarını ikiye bölerek, dairenin dışına ve içine birer 2n-gen çizelim. Bunların çevreleri de sırayla $latex a_{2n}$ ve $latex b_{2n}$ olsun. Arşimet’in formülleri şöyleydi:
$latex a_{2n} = 2 a_n b_n/(a_n + b_n)$
$latex b_{2n} = \sqrt{a_{2n} b_n}$
Altıgen için $latex a_6 = 4\sqrt{3}$, $latex b_6 = 6$ olur, bu değerlerden sırayla 12, 24, 48, 96 kenarlılara geçebiliriz. Bugün bir hesap makinesi veya bilgisayarınızdaki hesap tablosu yazılımı ile bu işlemi birkaç dakikada kolaylıkla yapabilirsiniz. Ama Arşimet’in hesap makinesi yoktu, ve bütün dehasına rağmen, hesaplama konusunda yaşadığı dönemden kaynaklanan handikaplara sahipti. O dönemde elle yüksek hassasiyette karekök almak çok zordu. En önemlisi, modern aritmetik notasyonunun ve Hint-Arap rakamlarının bize sağladığı kolaylıklardan yoksundu. Buna rağmen, Pi’nin 3 10/70 ve 3 10/71 arasında olduğunu belirleyebildi. Bu iki sınırın ortalamasını aldığınızda, dört basamak doğrulukla 3.14185… değeri elde edilir.
Arşimet’ten bir kuşak sonra Pergeli Apollonius’un Pi için 3.1416 değerini kullandığı ikincil kaynaklar aracılığıyla biliniyor, ancak orijinal eser kaybolduğu için Apollonius’un bu sonuca nasıl ulaştığı bilinmiyor. Ondan yüz yıl kadar sonra Batlamyus’un Almagest’inde de kullanılan bu yaklaştırım, yaklaşık bin yıl boyunca Avrupa’daki en hassas Pi değeri olarak kaldı.
Bu arada Çin’deki matematikçiler, muhtemelen batıdaki çalışmalardan bağımsız olarak, Pi’yi daha büyük doğrulukla hesaplama çabasını ileri götürdüler. Üçüncü yüzyılda Liu Hiu 3072 kenarlı bir çokgen kullanarak 3.14159 değerini elde etti. İki asır sonra Zu Chongzhi iki basamak daha ekleyerek Pi ‘nin 3.1415926 ve 3.1415927 arasında olduğunu bildirdi. Bu dâhi matematikçinin eserleri bugün kayıp olduğu için kullandığı yöntem bilinmiyor, fakat 12288 ($latex 3\times2^{12}$) kenarlı bir çokgen kullandığı tahmin ediliyor.
1400’lerin başında Semerkant’taki Uluğ Bey rasathanesinde çalışan hesap dâhisi Cemşit el-Kaşi’nin çalışması çıtayı çok yükseltti. El Kaşi $latex 3\times 2^{28}$ (805 milyon küsur) kenarlı bir çokgen kullandı, ki bu altıgenden başlayarak formülü 27 kere ilerletmek demekti (Arşimet 4 kere ilerletmişti). Bu ağır hesabın sonucunda Pi için 3.14159265358979 değerini elde etti. Virgülden sonra onbeş basamağa kadar doğru olan bu değerle, en uzak gezegen olan Neptün’ün yörüngesinin çevresini sadece bir santimetrelik hata payıyla belirlemek mümkündür (diğer ölçümlerin hata payının daha az olduğu varsayılarak). El Kaşi’nin başarısı o kadar büyüktü ki, neredeyse iki yüzyıl boyunca Pi için daha hassas bir değer üretilemedi.
Pi’nin sonraki rekoru Avrupa’da kırıldı. Ludolph van Ceulen (1540-1610), 15 kenarlı bir çokgenden başladı ve kenar sayısını otuzyedi defa iki katına çıkardı. 1596’da yayınladığı Pi değeri 20 haneye kadar doğruydu. Daha sonra kenar sayısını artırarak 35 hanelik hassasiyet sağladı. Öldüğünde bu sonuç mezar taşına yazıldı. Bu başarının etkisiyle bir dönem Almanya’da Pi sayısı “Ludolph sabiti” olarak anıldı.
Ludoph’un sonucu Arşimet yönteminin zirvesi oldu. Öğrencisi olan ünlü matematikçi ve fizikçi Willebrord Snell (1580-1626), dış çokgenlerin çevresinin çembere iç çokgenlerin iki katı hızla yakınsadığını gözledi. 1612’de yaptığı bir hesapta, 2 Pi’yi bulmak için iç ve dış çokgenlerin basit ortalamasını almak yerine, iç çokgen çevresinin 1/3’ü ile dış çokgen çevresinin 2/3’ünü topladı. Bu yöntemle Snell, bir 96-gen kullanarak Pi’yi dört basamak yerine yedi basamağa kadar doğru olarak hesaplayabildi.
Bu döneme kadar Pi için kullanılan algoritmik hesap yöntemi teorik analizde kullanmaya elverişli değildi. 1596’da Fransız matematikçi François Viète’nin Pi için verdiği formül yeni bir yaklaşımın habercisi oldu:
$latex \frac2\pi=
\frac{\sqrt2}2\cdot
\frac{\sqrt{2+\sqrt2}}2\cdot
\frac{\sqrt{2+\sqrt{2+\sqrt2}}}2\cdots$
Bu formülün önemi, hesaplama kolaylığından ziyade Pi için teorik bir ifade sağlamasındadır. Analiz ve trigonometrideki ilerlemeler sayesinde Pi için yeni formüller üretilmesiyle, çokgenler yönteminin miadı dolmuş oldu.
1655’de John Wallis Pi için bir sonsuz çarpım ifadesi yayınladı:
$latex \frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot\frac{6}{5} \cdot\frac{6}{7} \ldots$
Bu dönemde trigonometri işlemlerine dair sonsuz seri açılımları da keşfedilmişti. Sözgelişi, arktanjant (tanjantın tersi) fonksiyonunun şu ifadesi biliniyordu:
$latex \arctan x = x – \frac{x^3}{3} + \frac{x^5}{5} – \frac{x^7}{7} + \frac{x^9}{9} – \ldots $
Bu ve benzeri trigonometri fonksiyonlarının açılımı çok daha önce, Hint matematikçi ve astronom Madhava (1340-1425) tarafından keşfedilmişti. Radyan cinsinden $latex \pi/4$ (45 derece) açısının tanjantı 1 olduğundan, yukarıdaki seride x yerine 1 konularak Pi için bir sonsuz toplam bulunabileceği de Madhava’nın gözünden kaçmamıştı.
$latex \frac{\pi}{4} = 1 – \frac{1}{3} + \frac{1}{5} – \frac{1}{7} + \frac{1}{9} – \ldots $
Madhava sadece bunu değil, hesaplama açısından daha kolaylıklı olan başka formülleri de keşfetmişti. Madhava’nın çok üstün nitelikteki çalışmalarının Avrupa matematikçilerini ne kadar etkilediği kesin olarak bilinmiyor, fakat bu çalışmaların Cizvit misyonerler tarafından tercüme edilip Avrupa’ya aktarılmış olması kuvvetle muhtemel. Bu yüzden yukarıdaki ifadeye bugün Madhava-Gregory-Leibniz serisi adı veriliyor.
Bu serinin teorik çalışmalar için önemi var, ama hesaplama için pek faydalı değil. Ardışık terimler birbirlerine çok yakın büyüklükte olduklarından, toplamın Pi’ye yeterince yaklaşması için yüzbinlerce toplama yapmak gereklidir. Ama arktanjant serisi 1’den küçük değerler için çok daha çabuk yakınsar. Bu özelliği kullanarak, 1706’da John Machin verimlilik bakımından önceki bütün yöntemleri gölgede bırakan formüller yayınladı:
$latex \pi = 4 \arctan \frac{1}{2} + 4 \arctan \frac{1}{3} $
$latex \pi = 16 \arctan \frac{1}{5} – 4 \arctan \frac{1}{289} $
Bu formüllerde arktanjant fonksiyonu yukarıda verilen seri ile belli sayıda terim kullanılarak hesaplanır. Yüksek hassasiyet için daha fazla terim eklenmesi gerekir. Bu yöntemle Machin Pi’yi 100 basamağa kadar hesaplayabildi.
Bundan sonra Pi’yi hesaplamak pratik bir ihtiyaç olmaktan çıkmıştı, ama Pi’nin çekiciliği azalmadı. Hesapçılar seri açılıma dayalı formülleri kullanarak yeni ve daha doğru değerler sunmaya devam ettiler. Johann Dase (1824-1861) Pi’yi 200 basamağa kadar hesapladı. 1853’de amatör matematikçi William Shanks 707 basamağa ulaştığını ilân etti. Bir hesap hatası yüzünden bulduğu sonucun sadece ilk 527 basamağı doğruydu, ama bu hata 1945’de mekanik hesap makineleri kullanılana kadar farkedilmedi.
Yirminci yüzyılın ortasından itibaren, bilgisayar teknolojisinin ortaya çıkması sayesinde Pi tutkusu çok ilerilere götürülebildi. Ünlü ENIAC bilgisayarı ile 1949’da 2 037 basamağa ulaşıldı, ve basamak sayısı düzenli olarak artırıldı. Özellikle 1980’lerde her yıl birkaç kez rekor kırılıyordu. Ayrıntılı bir dökümü Wikipedia’da bulabilirsiniz.
Otomatik hesaplama imkânının yanı sıra, daha az terimle daha yüksek doğruluklu değerler veren formüllerin geliştirilmesi de Pi’nin hesaplanmasını ileriye götürdü. Sözgelişi, Hint matematikçi Ramanujan’ın 1910’da keşfettiği formül gibi:
$latex \frac {1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^\infty \frac {(4k)!(1103 + 26390k)}{(k!)^4 396^{4k}}$
Bu formülün her terimi, sonuca yaklaşık sekiz basamak doğruluk ekliyordu. 1985’de Bill Gosper bu yöntemle Pi’yi 17 milyon basamağa ulaştırdı.
Ramanujan formülü, Machin formülü, ve benzeri seri toplamlarına dayanan “klasik” algoritmalarda, doğruluğu iki katına çıkarmak için algoritmadaki adım sayısını iki katına çıkarmalısınız. 1976’da keşfedilen Salamin-Brent algoritması ise, her adımda doğru basamak sayısını iki katına çıkarabiliyordu, yani sonuçlar çok daha hızlı bir şekilde Pi’ye yaklaşıyordu. Bunun ardından her adımda doğru basamak sayısını üçe katlayan bir algoritma, dörde katlayan bir algoritma, ve dokuza katlayan bir algoritma keşfedildi.
Bir milyar basamak eşiği 1989’da Chudnovsky kardeşler tarafından kırıldı. Chudnovsky’ler kendi keşfettikleri, Ramanujan tarzı, “klasik” denebilecek bir formül kullandılar. Evlerinde kendi inşa ettikleri süperbilgisayarlarında yaptıkları hesaplamayla 1991’de 2 milyar, 1994’de ise 4 milyar basamağı geçtiler.
Tokyo Üniversitesi’nden Yasumasa Kanada, çalışma arkadaşlarıyla birlikte 1980’lerden beri Pi’nin birçok rekor hesaplamasına imza atmıştı, 2002’de bir trilyon basamağa ulaşan da o oldu. 2009’da Daisuke Takahashi 2,5 trilyon basamağı geçti.
Bu aşamaya kadar bütün rekor hesaplamalar süperbilgisayarlarla yapılmıştı. Daha sonraki üç rekor ise piyasada yaygın olarak bulunan donanımla hesaplandı. 2009 sonunda Fransa’da Fabrice Bellard, alelade bir masaüstü bilgisayar kullanarak Pi’yi 2,7 trilyon basamağa ilerletti. Shigeru Kondo, özel olarak hazırladığı güçlü bir bilgisayarda Alexander Yee’nin yazılımını çalıştırarak 2010 ortasında 5 trilyon basamağa çıktı. Kondo ve Yee 2011 Ekiminde 10 trilyon basamağa ulaştıklarını ilân ettiler.
Neden bu kadar ileri gidiliyor? Her türlü uygulama için 39 basamak yeterliyken, 10 trilyona çıkma takıntısı neden?
Pi hevesinin bir kısmı her insanın içindeki ileri gitme arzusu. Everest’e neden çıktıysak, Güney Kutbu’na ve Ay’a neden ayak bastıysak, Pi’yi de aynı sebeple kovalıyoruz. Ancak pratik sebepler de önemli rol oynuyor: Pi’yi bu akılalmaz hassasiyette hesaplamak için çok büyük sayıların doğru şekilde saklanması, işlenmesi, dönüştürülmesi gibi işlemler gerekiyor. Bu ağır işler süperbilgisayarların bile sınırlarını zorluyor, dolayısıyla da onların performansını test etme imkânı veriyor. Programları hazırlarken de büyük hesaplama işlerini yapabilmek için bilgisayarları nasıl verimli kullanabileceğimizi öğreniyoruz ve bu bilgiyi başka hesaplama problemleri için kullanabiliyoruz.
Pi’yi hesaplatarak bir bilgisayarda üretim hatası olup olmadığını da test edebiliriz. En ufak bir hata hesabın sonucunun yanlış olmasına yol açacaktır. Elde edilen sonucu bağımsız bir hesabın sonucuyla karşılaştırdığımızda arada fark görüyorsak, işlem birimlerinde bir sorun olduğundan şüphelenebiliriz. Sözgelişi 1986’da Cray-2 süperbilgisayarlarındaki bir donanım hatası Pi hesaplamaları ile ortaya çıkarıldı.
Pi için gereken trilyonlarca basamaklık aritmetik işlemleri, verimli aritmetik algoritmaları üretilmesine de vesile oldu. Sözgelişi, büyük sayıların çarpımı için, Fourier dönüşümüne dayalı özel bir algoritma, ilkokulda öğrendiğimiz çarpmaya göre çok daha hızlı sonuç veriyor. Bu ve benzeri algoritmaların bilimsel hesaplamada Pi’nin ötesinde birçok kullanım alanı var.
Pi, matematiksel bilimlerde sık sık, bazen de çok şaşırtıcı bir şekilde karşımıza çıkar. İşte bunlardan bir seçki.
- Kare sayıların terslerinin toplamı: $latex \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \ldots = \frac{\pi^2}{6}$
- Rastgele seçilen iki tamsayının ortak böleni olmaması ihtimali, yukarıdaki toplamın tersine, yani $latex \frac{6}{\pi^2} \approx 0.61$ değerine eşittir.
- Sadece tek sayıların karelerinin terslerinin toplamı: $latex \frac{1}{1^2} + \frac{1}{3^2} + \frac{1}{5^2} + \ldots = \frac{\pi^2}{8}$
- Benzer şekilde
$latex \frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \ldots = \frac{\pi^4}{90}$
$latex \frac{1}{1^6} + \frac{1}{2^6} + \frac{1}{3^6} + \ldots = \frac{\pi^6}{945}$
ve saire. Genel olarak, tamsayıların çift kuvvetlerinin terslerinin toplamı, Pi’nin aynı kuvvetine orantılıdır. Bu toplamların genel hali Riemann zeta fonksiyonu olarak bilinir. - İstatistikteki ünlü çan eğrisinin altında kalan alan Pi’nin kareköküne orantılıdır:
$latex \int_{-\infty}^{\infty} e^{-x^2} \mathrm{d}x = \sqrt{\pi}$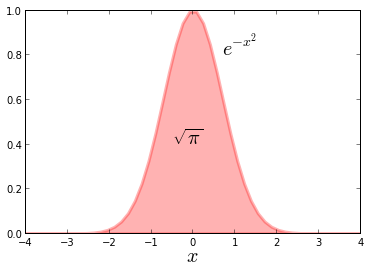
Çan eğrisi ve altında kalan alan. - Matematiğin en güzel formüllerinden biri dört temel sayıyı birleştirir
$latex e^{i\pi} + 1 = 0$
Burada i sanal sayı birimi, yani $latex \sqrt{-1}$, $latex e=2.718$.. ise neredeyse Pi kadar meşhur başka bir matematiksel sabittir.Buffon iğnesi: Zemine düzgün aralıklarla paralel çizgiler çizdiğinizi varsayın, ve uzunluğu çizgiler arasındaki mesafe kadar olan bir iğneyi yere atın. İğnenin çizgilerden biriyle kesişme ihtimali $latex 2/\pi$ olur.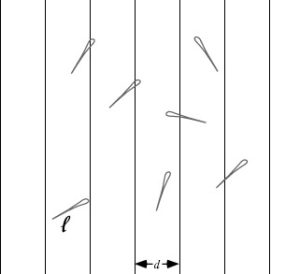
Buffon iğnesi: Rastgele fırlatılan iğnelerin kaç tanesinin çizgileri kestiğine bakarak Pi sayısı tahmin edilebilir. (Wolfram MathWorld)
Pi’nin ortaya çıktığı belki en garip yer, bir duvarda sonlanan bir hat üzerinde hareket eden iki topun çarpışmalarının sayısındadır. Topların biri ağır, öbürü daha hafif olsun. Hafif top başlangıçta durmaktadır, ağır top ise ona doğru hızla gelmektedir. Çarpıştıklarında hafif top hızla ileri itilir, ağır top ise biraz yavaşlar. Hafif top duvara çarparak geri gelir, ağır topla tekrar çarpışır, geri yansır, ağır top birazcık daha yavaşlar. Ardarda gelen çarpışmalardan sonra ağır top sonunda duracak ve geri dönecektir.

Ağır topun durmasına kadar kaç çarpışma gerektiği tabii topların kütle oranlarına bağlı. İki topun kütlesi eşitse sadece üç çarpışma olacaktır: Toplar çarpışır, birinci top durur; ikinci top duvara çarpıp döner; iki top yine çarpışır, ikinci top durur, birincisi ters yöne uçar gider.
Matematikçi Gregory Galperin, çok özel kütle oranları kullanılırsa, çarpışma sayılarının Pi’nin rakamlarını verdiğini ispatladı. Eğer birinci cisim ikincinin $latex 100^N$ katı kütleye sahipse, çarpışma sayısı Pi’nin ilk N+1 basamağıyla yazılan sayı kadar olur.
Sözgelişi, kütleler aynıysa (yani N=0 ise), toplam 3 çarpışmadan sonra birinci top uzaklaşıp gider. Ağır top hafifin 100 katı ağırlıktaysa (yani N=1) ise toplam 31 çarpışma, 10 000 katı ağırlıktaysa toplam 314 çarpışma gerçekleşir, ve böyle gider.
Ağır top olarak Dünya’yı, hafif top olarak da küçük bir kum tanesini alsak, Pi’nin ancak ilk onbeş basamağını elde ederiz, yani bu yöntem Pi’yi hesaplamak için kullanılamaz. Yine de sonucun güzelliği hayranlık uyandırıcı.
Kaynaklar
- The Penguin Dictionary of Curious and Interesting Numbers, David Wells.
- A History of Mathematics. Carl Boyer, Uta Merzbach.
- Wikipedia: Pi, Pi’nin yaklaşık değerleri, Pi’nin hesaplanma kronolojisi
- The Quest for Pi. David H. Bailey vd., Mathematical Intelligencer, V. 19, no. 1, 1997.
- Pi’nin dört milyon basamağını buradan indirebilirsiniz.
- Yetmediyse, bir milyar basamaklı değeri burada.
- Arşimet’in Pi formülü, Wolfram MathWorld.
- Craig Wood Arşimet yöntemini başka bir formülle kullanmış. Sitede Pi’yi başka yöntemlerle hesaplamanın ayrıntıları da yer alıyor.
- Çarpışan toplar ve Pi bağlantısı: Playing Pool with $latex \pi$, G. Galperin, Regular and Chaotic Dynamics, V.8, no. 4, 2003. Math StackExchange‘de yöntem biraz daha iyi açıklanmış.


çok aydınlatıcı ve çok güzel öğretmenelr hep piyi üç alalım dio ve piyi sorunca konumuzla alakalı deil deip geçio
bizim öğretmenimiz bize açıklayınca çok şaşırmışştık…..
bunu çıkardığınız için tesekkürler
Ağır top olarak Dünya’yı, hafif top olarak da küçük bir kum tanesini alsak, Pi’nin ancak ilk onbeş basamağını elde ederiz
denmiş. Bu söz yazanın ne dediğini düşünmeden yazdığı, mahallenin delisinin saçmasıdır! Uzayda duran cisim hayal etmek zor da olsa hadi bunu sineye çekip, diyelim Güneş’e göre duran cisim, bir kiloluk kaya ‘sözde’ duruyor olsun. Dünya kayaya yaklaşırken, kaya durmaya devam etmez ve etkinin hissedildiği bir mesafe alanı içine girilince Dünya’nın çekimine kapılıp Dünya’ya doğru hareket etmeye başlar ve Dünya’ya düşer ve bir daha da çarpmanın etkisi ile geri zıplayıp Dünya’dan ayrılamaz. Bu hesabı yapanlar, sanki çarpan toplardan küçük olan ve sözde durağan farzedileni, çarpana değin kımıldamadan öylece duruyor diye nasıl fiziğe aykırı şekilde farzebiliyor ve hayalden olmayan fizik kuralları icadedip saçmalamışlar. Ayrıca toplar sanki yatay zeminde farzedilmiş, düz yüzey yeterince uzun olsa, diyelim 100 veya 1000 kilometre olsa uzaydan bakılınca bu düz olmaz ve kesik çember olur ve ancak bu şekilde Dünya’nın çekim alanı toplara göre etkisiz kılınabilir yani tamamen düz zemin toplara göre eğik düzlem olur ve hesap tamamen şaşar zaten değil mi? Yatay sürtünme sıfır farzedilmesi ayrıca fizikte olmayan bir başka hayali faraza. Hülasa hayali topların, pinin rakamlarını vermesi olmayan hayali bir evrende hayranlık veren güzellik gibi görünse de, hakikatte bu bir yalan fantezidir unutmayın!
kaba üslubumu lütfen affedin, zaten annem beni azarladı.
bilardo topların kütle oranları büyük/küçük
256 katı ise 50 defa
65536 katı ise 804 defa
1677216 katı ise 12867 defa
1099511627776 katı ise 205887 defa çarpışıp gider gelirler.
tabii ki tamamen hayali ve hakikatte olmayan sürtünmesiz ideal bilardo masasında.
peki bu 50,804,12867,205887 vs nin bir manası var mı?
cevap: evet pi nin
3.243f6a8885a308d313198a2e03707344a4093822299f31d0082efa98ec…
şeklindeki 16 tabanlı hexadesimal yazılışında her bir hanedeki rakamların (16*16) üzeri +1 hanesinin sırasıyla desimal karşılıkları. ideal (yani hakiaktte olmayan) bilardo topu çarpışmasında, pi nin bu özelliği sadece onlar tabanına göre 3,1415926… yazılımına özgü bir özellik veya güzellik değil.
pi yi iki tabanına göre veya sekiz tabanına göre yazsak, üşenmezseniz deneyin, yine aynı özellik çıkar. netice: kullanmaya alışık olduğumuz onlar tabanı “özel” değildir ve pi ye özgü bu güzelliği sadece onlar tabanına ve sanki kendimize özgü olarak zannetmeyiniz!
yukarda bazı rakamları ve hatta hexadesimal haneyi yanlış tuşlamışım, şaşar beşer parmağıma takılmayın, hızlı hesap şaşmadı, kontrol edildi.
google da :
pi circle crop
diye arayınca gördüm ki, insan olmayan mahlukat, daireyi 10 eşit açıya bölüp, pi sayısını 10 haneye kadar kodlamış.
bilim adamı demek kızlara haksızlık diye üzülüyordum, şimdi bilim insanı deyince de birilerine haksızlık edildiğini gördüm.
en iyisi bilimci demek, böylece evrensel bilime meraklı olanların kümesini daha iyi tanımlarız.