Aceleniz var… Evden bir an önce çıkmanız lazım. Önemli bir evrakın evdeki açık pencereler arasında cerayan eden rüzgâr ile bir yerlere uçuştuğunu fark ediyorsunuz ve onu arıyorsunuz. Acaba nasıl bir arama yolunu tercih ederdiniz?
Ya da kalabalık bir konserde bir arkadaşınızı kaybettiniz. Üstelik telefonla da ulaşamıyorsunuz. Onu nasıl arardınız? Bir yerde bekler ve önünüzden geçmesini mi beklerdiniz? Yoksa her bir sırayı tek tek arar mıydınız? Ya da arkadaşınızı görme umuduyla rastgele bir arama davranışı mı izlerdiniz?
Şimdi başka sorular:
Bu arama hareketlerinizin tüm insanlara özgü bir matematiksel ya da istatistikî bir örüntüsü olur muydu?
Elbette kendi evini tanıyan ve bilen, evrakın nereye uçması halinde onu göremiyor olabileceğinizi kestirebilen siz, sahip olduğunuz bilişsel kabiliyetlerle evinize uygun ve size özgü bir örüntüyü takip ederdiniz. Ya da arkadaşınızın uzun boylu olması, hoparlöre yakın yerleri tercih etmemesi, ya da sigara kullanıcısı olması gibi bilgileri kullanarak arama kriterlerine sahip olabilirdiniz.
Peki ya bir arı, ton balığı ya da köpekbalığı olsaydınız ve bilinçli olarak kullanabileceğiniz veriler olmasaydı?
Rastlantı ve Düzen
Richard Feynman’ın tabiriyle doğa bir satranç oyunudur. Bilim insanları ise satranç oyununu izlerken onun kurallarını kestirmeye çalışan izleyicilerdir. Bu izleme esnasında taşların hangi hamleleri yaptığına yönelik hipotezler oluşturacaklardır ve bu hipotezlerini doğrulayan –ya da yanlışlayarak onu hipotezini güncellemeye götüren- hareketlerin de hep takipçisidirler (1).
Çevremizdeki etkileşimlerin kararlı bir doğası vardır. Bu yüzden çok ani ve olağanın dışında olaylar olmasını beklemeyiz. Mesela bir anda bulunduğumuz yerde havanın tükenmesinden ve nefessizlikten ölmekten endişe etmeyiz. Ya da odanın bir ucunda yanıyor halde duran sobanın bir anda her yere ateş kusmasından kaygı duymayız. Bu bakımdan baktığımızda her şey çok düzenlidir, hayatın “doğal akışı” bulunur.
Etrafımızdaki karmaşık dünyanın bu karmaşık ve çeşitli durum ve görünümlerine karşın onu büyük ölçüde kontrol edebiliyor olmamızın sebebi, bu doğal akışı sağlayan kuralların basitliğidir. Mesela kimyasal reaksiyonlar birkaç küçük kural dizgesi içerisinde gerçekleşirler; ama et kokar, sigara yanar, yemek pişer, yumurta rafadan olur… Bunlar küçük kuralların üstüste binerek oluşturduğu karmaşık görünümlerdir. (Çok küçük kuralların üstüste binerek daha kompleks kurallar varmışçasına makro yapılar oluşturabileceği ya da düzenli bir örüntü yaratabileceğine dair çeşitli örnekler ve modellerden dergimizde daha önce bahsetmiştik: Conway’in Hayat Oyunu ve Schelling Ayrışma Modeli gibi).
Bilim insanları bu kuralları merak ederler, ve böylece anlamak ve açıklayabilmek isterler. Sosyal bilimler “bilişsel” bir canlı olan insanı ve onun bir üyesi olduğu toplumu anlamaya yönelik amaçlar güdüyor olsalar da bu bilişsellik –ve doğal olarak belirsizliklerin kaynağı olan karar verme faktörü- sosyal bilimcileri zorlar. Buna keza bilişsel olmayan canlı varlıkların –ve dolayısıyla cansız varlıkların- hareketleri karar verme –ve böylece sapma- eyleminden uzak, bu sayede de anlaşılabilir, incelenebilir ve kimi zaman net olarak açıklanabilir haldedirler. Bu sayede “çoğunlukla ve büyük ölçüde” bilişsel davranmadıklarını varsaydığımız hayvanlar alemi kendi evrimleri içerisinde sahip oldukları strateji ve davranış örüntüleri açısından ilgi çekicidirler. Bilişsel bir sürecin ürünü olmayan ve içgüdü olarak adlandırdığımız davranış örüntüleri çoğu zaman hayvanların varkalımlarında önemli bir yere sahiptirler ve “En Kararlı Strateji” olarak adlandılılırlar (2). Tarih boyunca biyolog ve zoologların da aralarında olduğu bilim insanları bu stratejilerle ilgilenmişlerdir ve konu strateji olduğundan belki de, matematikçiler de bu grup arasındadır: Ünlü bilim insanı John Nash’in hayatını konu alan Akıl Oyunları adlı filmi sevenler, John Nash’in bir ara güvercinlerin hareketlerini çözmeye gayret ettiğini hatırlayacaklardır. Yeri gelmişken bahsedelim; bu yazıda bahse konu olan Paul Lévy de bir matematikçiydi –her ne kadar Lévy Yürüşüyü ile yiyecek arama hipotezi ona ait olmasa da-.
Lévy Yürüyüşü
Bu yazının konusu olan Lévy yürüyüşü, bazı hayvanların kullandığı yemek arama stratejilerinden birini ifade etmektedir ve adım uzunlukları bir sürekli olasılık dağılımına uygun olarak gerçekleşen hareket örüntüsünü ifade eder. Lévy dağılımı aslında sürekli bir olasılık dağılımıdır. Eğer fiziksel bir olgu için bir olasılık dağılımından bahsediyorsak, akıllara ayyaş yürüyüşü olarak da anabileceğimiz rastgele yürüyüş (random walk) gelir.
Zilzurna sarhoş olmuş birisinin rastgele adımlar attığını düşünün. Her adımda sağa, sola, ileri, veya geri gitme ihtimali aynı olsun. Bu “ayyaş”ın hareketi, fiziksel dünyadaki birçok sistemin davranışı için bir model oluşturuyor, sözgelişi suyun içindeki polenlerin hareketi, parfüm kokusunun havada yayılması, uzun molekül zincirlerinin büyümesi, hisse senetlerinin değerlerinin değişmesi gibi (3).
Levy yürüyüşü de bir rastgele yürüyüş örneğidir. Rasgele yürüyüş yere bıraktığımız bir topun yapacağı hareketteki gibi formüle edilebilen ve tahmin edilebilir bir matematiksel modele değil, hareketlerin bir takım sınırlar ya da kurallar nedeniyle bir olasılık dağılımına uyduğu istatistik bir model sunar bizlere.
Basit bir örnek vermeye çalışalım:
Annelerimiz genellikle ne yemek yapacaklarına rastgele olarak karar verirler. Bu yemeklerden bir kısmını yapmak çok zahmetli, bir kısmı ise çok kolaydır. Tabi bir de besleyicilik ya da sağlıklı olması açısından başka bir değerlendirme yapmak da mümkündür. Örneğimizdeki annenin çalışan bir kadın olduğunu varsayalım: Zaman yönetimi onun için önemlidir ama çocuğunun iyi beslenmesini de sağlamak istemektedir. Bu annenin hangi yemeği yapacağına yönelik kesin bir bağıntı geliştirmek ve bu yönde bir tahminde bulunmak mümkün değildir, ancak belirli bir süre zarfında hangi yemekleri yaptığını inceleyerek onun seçimlerinin bir olasılık dağılımına uyup uymadığına bakabilir ve bir modele ulaşabiliriz.

Bu anne her ne kadar yemek yapmaya rastgele karar veriyorsa da zamanla ve besleyicilikle ilgili kaygıları nedeniyle ortaya böyle bir tablo çıkıyorsa; bir ucunda besleyici ama zor, diğer ucunda kolay ama besleyici olmayan yemeklerin yer aldığı bir normal dağılım elde edebiliriz. Mesela omlet çok hızlı yapılabilir, ama tek başına yeteri kadar besleyici ya da lezzetli değildir. Bu yüzden ele alınan zaman zarfında bir kez yapılmıştır. Öte yandan güveç gibi bir yemek de içeriği sebebiyle oldukça zengin ve besleyici olabilir; ancak o da çok zahmetlidir. O yüzden o da sadece bir sefer yapılmış olabilir. Nispeten daha zor ama daha besleyici ya da nispeden daha besleyici ama daha zor yemeklerden optimum olanlara daha sık rastlanması beklenir.

İşte Lévy Yürüyüşü olarak adlandırdığımız davranış da -yemeklerin pişirilme sayıları gibi- hayvanların iki yiyecek arama/toplama eylemi arasında kat ettikleri mesafelerin Lévy dağılımı ya da Cauchy dağılımı gibi uzun etekli (ya da yoğun kuyruk) sürekli olasılık dağılımlarına uygun olarak gerçekleşen davranıştır. Lévy dağılımı da tıpkı normal dağılım gibi sürekli olasılık dağılımıdır ancak bu dağılımı ortaya çıkaran bir takım varsayım, değer ve koşullar onu normal dağılımdan farklı kılar.
Sürekli olasılık dağılımıyla ilgili bir örnek Vikipedi’den:
Bir sürekli olasılık dağılımında değerler sürekli olan bir açıklıkta tanımlanır ve tek bir değer için olasılık sıfıra eşittir. Örneğin bir okçuluk sahasında atılan bir okun hedef tahtasında tek bir noktaya düşmesi olasılığı sıfırdır; çünkü geometri kuramına göre bir noktanın ne eni ne de boyu bulunmaktadır ve hedef üzerindeki varsayılan nokta sonsuz küçüklüktedir. Buna karşılık, atılan okun hedef üzerinde belli bir alana düşmesi olasılığı bulunabilir. Böylece hedefe ok atma olayında hedef tahtasının her bir alanına okun düşme olasılığını tanımlayan bir düzgün fonksiyon olasılık yoğunluk fonksiyonu (OYF), bu olayın olasılık dağılımını tanımlar. Olasılık yoğunluk fonksiyonun altında kalan alan (yani integrali), hedef tahtasının tümünü (belki de yakınındaki bir duvar parçasını da) kaplayan alanı kapsadığı için, bire eşit olacaktır; çünkü atılan okun mutlaka bir alana gitmesi gerekmektedir (4).
Diğer tür olan ayrık olasılık dağılımı öyle değildir: Örneğin tek bir zar atıyor olalım. Bütün olasılıklar ayrı olayları temsil ederler ve birbirine eşitlerdir. Üstelik ilk atışımda zarın kaç gelmiş olduğu sıradaki hamlemde kaç geleceğini etkilemeyecektir. Her bir olayın tekil olarak olasılıkları bellidir ve zar “daha önce kaç kez altı geldim acaba?” diye düşünmeyecektir. Dolayısıyla sürekli bir dağılımdan bahsedilemez ve yukarıda görmüş olduğumuz gibi dağılım modelleri elde edilemez.
Yemek Arama Modeli
Şimdi gelelim yiyecek arayan bir bal arısının davranışına…
Çiçek arayan bir arının enerjisi sınırlıdır. Çevredeki kaynaklar da öyle. Ayrıca arada bir rastgele bir noktaya ışınlanmadığına göre bir önceki konumu ile sıradaki konumu birbirine bağlıdır. Peki bir arı belli bir bölgedeki çiçekleri kontrol ettikten sonra, sıradaki konumunu nasıl belirleyecektir ve nereyi tercih edecektir? Arılar bölgeleri sırayla mı aramaktadır? Yoksa rastgele mi? Rastgele arıyorlarsa kat ettikleri mesafe bir dağılım modeline uyuyor mudur?
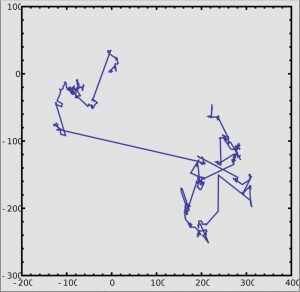
Evet! Belki çoğumuzun daha önce görerek tespit ettiği üzere, bir balarısı yiyecek arayacağı bölgeye ulaşır ve bir çiçeğe bakar. Derken kısa bir uçuş yaparak aynı alandaki diğer çiçeğe geçer. Bu küçük alanda bir miktar kısa uçuşlar yaptıktan sonra bu defa rastgele bir yön seçer ve biraz daha uzun bir uçuş gerçekleştirerek başka bir bölgeye geçer. Buradaki aramalarında da bir miktar kısa uçuşlar gerçekleştirir ve akabinde tekrar bir uzun uçuş daha yapar. Yuvasına dönene dek bu döngü devam eder.
Araştırmalar aralarında arılar, ton balıkları ve köpek balıklarının da olduğu pek çok hayvanın yiyecek arama davranışlarında kat ettikleri mesafenin Lévy dağılımına uygun olduğunu gösteriyor.
Bu stratejiin varlığı görgül kanıtlarla desteklendiğine göre sıra bunun neden olduğu sorusunun yanıtına geliyor. Bazı araştırmacılar “neden” sorusuna da eğilmişler ve şu yanıta ulaşmışlar: Optimum enerji sarfiyatı.
Rassal yiyecek aramalarında zaman / enerji açısından optimum stratejinin ne olabileceğine yönelik araştırmalar Lévy dağılımı gibi olasılık dağılımlarına uygun davranış örüntülerinin en iyi strateji olabileceğini gösterdiler (5). Bilim insanları bu araştırmalarda konum ve hız bilgilerini ileten bir takım sensörleri hayvanlar üzerine yerleştirerek gerçek datalar ile görgül kanıtlar sağladılar. Henüz 2010 yılında yapılan ve milyonlarca konum verisine dayanan okyanus araştırmaları bazı okyanus balıklarının yaşadıkları bölgeye göre değişiklik göstermek üzere Lévy da da Brown dağılımlarını kullandığını gösterdiler (6).
VE İNSAN!
Her ne kadar bugün yiyecek aramak bizler için çevremize ya da Yemek Sepeti’ne bakıp “nerede yesek acaba” ya da buzdolabına bakıp “ne pişirsem acaba” eylemlerine indirgenmiş olsa da geçmişte böyle değildi. Günümüzde de avlanarak ya da toplayıcı olarak yaşayan insan toplulukları bulunmakta.

23 Aralık’ta Arizona Üniversitesi’nden Antropolog David Raichlen ve Herman Pontzer’in başında olduğu bir ekip tarafından kaleme alınan ve Proceedings of the National Academy of Sciences dergisinde yayınlanan Evidence of Lévy walk foraging patterns in human hunter-gatherers adlı araştırma, Lévy yürüyüşü olarak bilinen ve bugüne dek arılar ve köpek balıklarının kullandığı düşünülen bir yiyecek arama stratejisinin avcı toplayıcı insanlar tarafından da kullanılmış olabileceğini öne sürüyor (7).
David Raichlen, Herman Pontzer ve ekibi bu çalışmalarını Tanzanya sınırları içerisinde yaşayan Hadza kabileleri üzerinde gerçekleştirmiş, çünkü Hadza insanları hala geleneksel yöntemlerle avlanıyorlar. Araştırma kapsamında avcıların avlarını ararken gerçekleştirdikleri hareketler GPS ile incelenerek profilleri çıkarılmış ve bu profiller incelendiğinde Hadza insanlarının da av arama davranışlarında Lévy yürüyüşü gerçekleştirdikleri görülmüş.
Geleneklerinden çok vazgeçmemiş olan Hadza insanlarının avcı toplayıcı atalarımız hakkında fikir verebileceğine inanan ekip tarihe ışık tutabilecek bir takım araştırmaların önünü açmış oluyor. Ayrıca bu keşif insan ve diğer hayvanlar arasında matematiksel bir köprü kurmuş olduğu gibi, rastgele görünen davranışlarımızın ardındaki evrimsel mirasın varlığını hatırlatıyor…
Kaynaklar:
(1) – Richard Feynman – Altı Kolay Parça (Evrim Yayınları)
(2) – Richard Dawkins – Gen Bencildir (TÜBİTAK Yayınları)
(3) – Kaan Öztürk – Açık Bilim: Ayyaş Yürüyüşü
(4) – Vikipedi – Sürekli Olasılık Dağılımları maddesi
(5) – Viswanathan G. M. et al http://www.nature.com/nature/journal/v401/n6756/full/401911a0.html akt. Wikipedia (“Lévy flight foraging hypothesis” maddesi.)
(6) – Humphries N. et al http://www.nature.com/nature/journal/v465/n7301/full/nature09116.html akt. Wikipedia (“Lévy flight foraging hypothesis” maddesi.)
(7) Science Daily – “Walking the Walk: What Sharks, Honeybees and Humans Have in Common”


Yorum Ekle